【题目】如图所示,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

参考答案:
【答案】(1)30°;(2)6.
【解析】试题分析:(1)根据平行线的性质可得∠EDC=∠B=60°,根据三角形内角和定理即可求解;
(2)易证△EDC是等边三角形,再根据直角三角形的性质即可求解.
试题解析:解:(1)∵△ABC是等边三角形,∴∠B=60°,∵DE∥AB,∴∠EDC=∠B=60°,∵EF⊥DE,∴∠DEF=90°,∴∠F=90°﹣∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,∴△EDC是等边三角形,∴ED=DC=3,∵∠DEF=90°,∠F=30°,∴DF=2DE=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的每个内角的度数都是108°,那么这个多边形的边数是( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
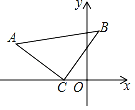
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点A的坐标为(﹣6,3),求点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,两条直线的位置关系是( )
A.平行和垂直B.平行和相交C.垂直和相交D.平行、垂直和相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①a为任意有理数,a2+1总是正数;②如果a+|a|=0,则a<0;③两点确定一条直线;④若MA=MB,则点M是线段AB的中点.其中正确的有( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,二次函数y=mx2+nx-2的图象过A(-1,-2)、B(1,0)两点.
(1)求此二次函数的解析式并画出二次函数图象;
(2)点P(t,0)是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的( )
A. 三条中线的交点 B. 三边垂直平分线的交点
C. 三条高的交点 D. 三条角平分线的交点
相关试题

