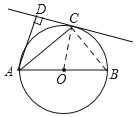
【题目】如图,AB为⊙O的直径,点C在⊙O上,AD⊥CD于点D,且AC平分∠DAB,求证:
(1)直线DC是⊙O的切线;
(2)AC2=2ADAO.

参考答案:
【答案】(1)证明见解析.(2)证明见解析.
【解析】(1)连接OC,由OA=OC、AC平分∠DAB知∠OAC=∠OCA=∠DAC,据此知OC∥AD,根据AD⊥DC即可得证;
(2)连接BC,证△DAC∽△CAB即可得.
(1)如图,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠OAC=∠DAC,
∴∠DAC=∠OCA,
∴OC∥AD,
又∵AD⊥CD,
∴OC⊥DC,
∴DC是⊙O的切线;
(2)连接BC,
∵AB为⊙O的直径,
∴AB=2AO,∠ACB=90°,
∵AD⊥DC,
∴∠ADC=∠ACB=90°,
又∵∠DAC=∠CAB,
∴△DAC∽△CAB,
∴![]() ,即AC2=ABAD,
,即AC2=ABAD,
∵AB=2AO,
∴AC2=2ADAO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,已知
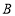 、
、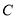 两点把线段
两点把线段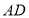 分成
分成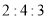 三部分,
三部分,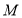 是
是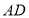 的中点,若
的中点,若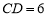 ,求线段
,求线段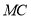 的长.
的长. 
(2)如图
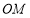 、
、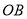 、
、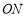 是
是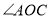 内的三条射线,
内的三条射线,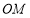 、
、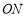 分别是
分别是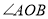 、
、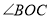 的平分线,
的平分线,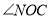 是
是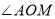 的3倍,
的3倍,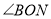 比
比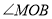 大
大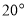 ,求
,求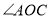 的度数.
的度数. 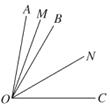
-
科目: 来源: 题型:
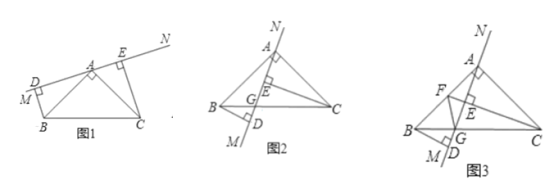
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=90°,AB=AC.MN是过点A的直线,BD⊥MN 于D,CE⊥MN于E.
(1)求证:BD=AE.
(2)若将MN绕点A旋转,使MN与BC相交于点G(如图2),其他条件不变,求证:BD=AE.
(3)在(2)的情况下,若CE的延长线过AB的中点F(如图3),连接GF,求证:∠AFE=∠BFG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形
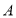 的边长是1米;
的边长是1米;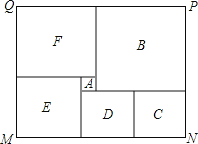
(1)若设图中最大正方形
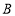 的边长是
的边长是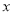 米,请用含
米,请用含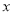 的代数式分别表示出正方形
的代数式分别表示出正方形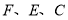 的边长
的边长(2)观察图形的特点可知,长方形相对的两边是相等的(即
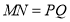 ,
, 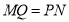 )请根据以上结论,求出
)请根据以上结论,求出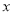 的值
的值(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
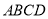 中,
中,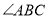 和
和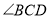 的平分线交于
的平分线交于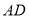 边上一点
边上一点 ,且
,且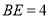 ,
,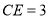 ,则
,则 的长是( )
的长是( )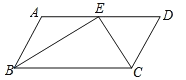
A.3B.4C.5D.2.5
-
科目: 来源: 题型:
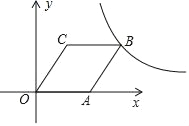
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x轴的正半轴上,顶点C的坐标为(1,
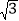 ).
).(1)求图象过点B的反比例函数的解析式;
(2)求图象过点A,B的一次函数的解析式;
(3)在第一象限内,当以上所求一次函数的图象在所求反比例函数的图象下方时,请直接写出自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐对几何中角平分线的兴趣浓厚,请你和乐乐一起探究下面问题吧.已知
 °,射线
°,射线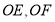 分别是
分别是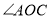 和
和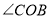 的平分线;
的平分线;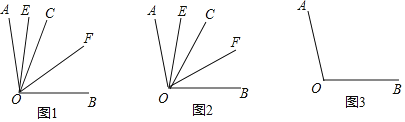
(1)如图1,若射线
 在
在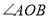 的内部,且
的内部,且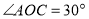 ,求
,求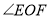 的度数;
的度数;(2)如图2,若射线
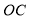 在
在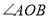 的内部绕点
的内部绕点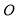 旋转,则
旋转,则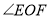 的度数为;
的度数为;(3)若射线
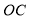 在
在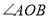 的外部绕点
的外部绕点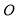 旋转(旋转中
旋转(旋转中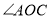 ,
,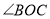 均指小于
均指小于 的角),其余条件不变,请借助图3探究
的角),其余条件不变,请借助图3探究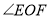 的大小,请直接写出
的大小,请直接写出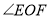 的度数(不写探究过程)
的度数(不写探究过程)
相关试题

