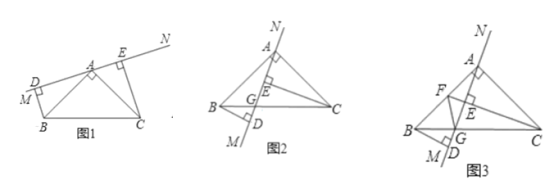
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC.MN是过点A的直线,BD⊥MN 于D,CE⊥MN于E.
(1)求证:BD=AE.
(2)若将MN绕点A旋转,使MN与BC相交于点G(如图2),其他条件不变,求证:BD=AE.
(3)在(2)的情况下,若CE的延长线过AB的中点F(如图3),连接GF,求证:∠AFE=∠BFG.
参考答案:
【答案】(1)证明见详解;(2)证明见详解;(3)证明见详解.
【解析】
(1)首先证明∠1=∠3,再证明△ADB≌△CEA,然后根据全等三角形的性质可得BD=AE;
(2)首先证明∠BAD=∠ACE,再证明△ABD≌△CAE,根据全等三角形对应边相等可得BD=AE;
(3)首先证明△ACF≌△BAP,然后再证明△BFG≌△BPG,再根据全等三角形对应角相等可得∠BPG=∠BFG,再根据等量代换可得结论∠BFG=∠AFE.
证明:(1)如图,
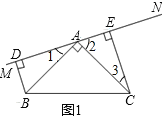
∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∵∠BAC=90°,
∴∠1+∠2=90°,
又∵∠3+∠2=90°,
∴∠1=∠3,
在△ADB和△CEA中,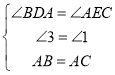 ,
,
∴△ADB≌△CEA(AAS),
∴BD=AE;
(2)如图,
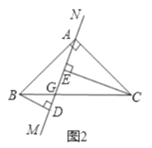
∵BD⊥MN,CE⊥MN,
∴∠BDA=∠CEA=90°,
∵∠BAD+∠CAE=90°,∠ACE+∠CAE=90°,
∴∠BAD=∠ACE,
在△ABD和△CAE中,
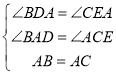
∴△ABD≌△CAE(AAS),
∴BD=AE;
(3)过B作BP∥AC交MN于P,
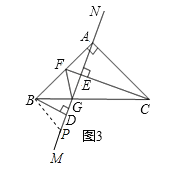
∵BP∥AC,
∴∠PBA+∠BAC=180°,
∵∠BAC=90°,
∴∠PBA=∠BAC=90°,
由(2)得:∠BAP=∠ACF,
∴在△ACF和△BAP中,
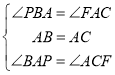
∴△ACF≌△BAP(ASA),
∴∠AFC=∠BPA,AF=BP
∵BF=AF,
∴BF=BP,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
又∵∠PBA=90°,
∴∠PBG=45°,
∴∠ABC=∠PBG,
在△BFG和△BPG中,
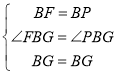
∴△BFG≌△BPG(SAS),
∴∠BPG=∠BFG,
∵∠BPG=∠AFE,
∴∠BFG=∠AFE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=60°,点P是∠AOB内的定点且OP=
 ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )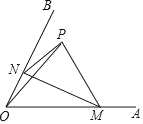
A.
 B.
B.  C. 6 D. 3
C. 6 D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,已知
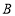 、
、 两点把线段
两点把线段 分成
分成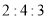 三部分,
三部分,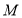 是
是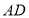 的中点,若
的中点,若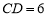 ,求线段
,求线段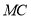 的长.
的长. 
(2)如图
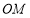 、
、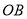 、
、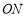 是
是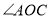 内的三条射线,
内的三条射线,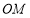 、
、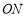 分别是
分别是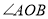 、
、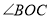 的平分线,
的平分线,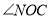 是
是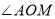 的3倍,
的3倍,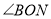 比
比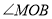 大
大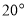 ,求
,求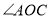 的度数.
的度数. 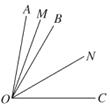
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形
 的边长是1米;
的边长是1米;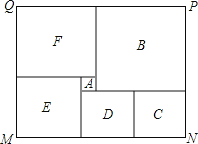
(1)若设图中最大正方形
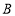 的边长是
的边长是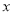 米,请用含
米,请用含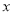 的代数式分别表示出正方形
的代数式分别表示出正方形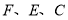 的边长
的边长(2)观察图形的特点可知,长方形相对的两边是相等的(即
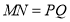 ,
, 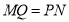 )请根据以上结论,求出
)请根据以上结论,求出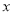 的值
的值(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O上,AD⊥CD于点D,且AC平分∠DAB,求证:
(1)直线DC是⊙O的切线;
(2)AC2=2ADAO.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
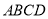 中,
中,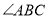 和
和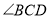 的平分线交于
的平分线交于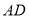 边上一点
边上一点 ,且
,且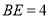 ,
,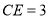 ,则
,则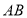 的长是( )
的长是( )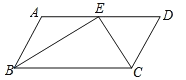
A.3B.4C.5D.2.5
相关试题

