【题目】在Rt△ABC中,∠A=90°,AC=AB=4, D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1 , 设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.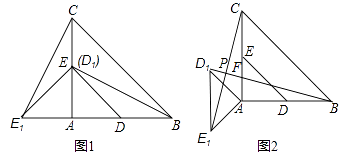
(1)如图1,当α=90°时,线段BD1的长等于 , 线段CE1的长等于;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1= CE1 , 且BD1⊥CE1;
(3)①设BC的中点为M,则线段PM的长为;②点P到AB所在直线的距离的最大值为 . (直接填写结果)
参考答案:
【答案】
(1)2 ![]() ;2
;2 ![]()
(2)
证明:当α=135°时,如图2,
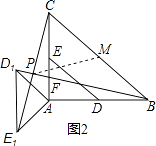
∵Rt△AD1E是由Rt△ADE绕点A逆时针旋转135°得到,
∴AD1=AE1,∠D1AB=∠E1AC=135°,
在△D1AB和△E1AC中
∵ 
∴△D1AB≌△E1AC(SAS),
∴BD1=CE1,且∠D1BA=∠E1CA,
记直线BD1与AC交于点F,
∴∠BFA=∠CFP,
∴∠CPF=∠FAB=90°,
∴BD1⊥CE1;
(3)2 ![]() ;1+
;1+ ![]()
【解析】解:(1)∵∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,
∴AE=AD=2,
∵等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1 , 设旋转角为α(0<α≤180°),
∴当α=90°时,AE1=2,∠E1AE=90°,
∴BD1= ![]() =2
=2 ![]() ,E1C=
,E1C= ![]() =2
=2 ![]() ;
;
所以答案是:2 ![]() ,2
,2 ![]() ;
;
3)解:①如图2,
∵∠CPB=∠CAB=90°,BC的中点为M,
∴PM= ![]() BC,
BC,
∴PM= ![]() =2
=2 ![]() ,
,
所以答案是:2 ![]() ;
;
②如图3,作PG⊥AB,交AB所在直线于点G,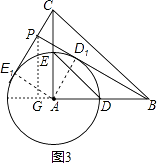
∵D1 , E1在以A为圆心,AD为半径的圆上,
当BD1所在直线与⊙A相切时,直线BD1与CE1的交点P到直线AB的距离最大,
此时四边形AD1PE1是正方形,PD1=2,则BD1= ![]() =2
=2 ![]() ,
,
故∠ABP=30°,
则PB=2+2 ![]() ,
,
故点P到AB所在直线的距离的最大值为:PG=1+ ![]() .
.
所以答案是:1+ ![]() .
.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和切线的性质定理的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知12箱苹果,以每箱10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,称重记录如下:
+0.2 ,—0.2,+0. 7,—0.3,—0.4,+0.6,0,—0.1,—0.6,+0.5,—0.2,—0.5。
⑴求12箱苹果的总重量;
⑵若每箱苹果的重量标准为10
 0.5(千克),则这12箱有几箱不合乎标准的?
0.5(千克),则这12箱有几箱不合乎标准的? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利 润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (单位:个)与
销售单价x(单位:元/个)之间的对应关系如图所示: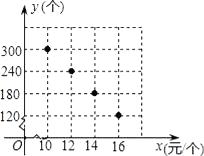
(1)y与x之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(单位:元)与销售单价x(单位:元/个)之间的函数关系式;
(3)在(2)问的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数
 ,
, 在第一象限内的图象如图所示,点P1,P2,P3,…,P2018在反比例函数
在第一象限内的图象如图所示,点P1,P2,P3,…,P2018在反比例函数 图象上,它们的横坐标分别是
图象上,它们的横坐标分别是 ,
, ,
, ,…,
,…, ,纵坐标分别是1,3,5,…,共2018个连续奇数,过点P1,P2,P3,…,P2018分别作
,纵坐标分别是1,3,5,…,共2018个连续奇数,过点P1,P2,P3,…,P2018分别作 轴的平行线,与
轴的平行线,与 的图象交点依次是Q1(
的图象交点依次是Q1( ,
, ),Q2(
),Q2( ,
, ),Q3(
),Q3( ,
, ),…,Q2018(
),…,Q2018( ,
, ),则
),则 =_________.
=_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 与
与 成正比例,且
成正比例,且 时,
时, .
.(1)求出
 与
与 之间的函数关系式;
之间的函数关系式;(2)在所给的直角坐标系(如图)中画出函数的图象;
(3)直接写出当
 时,自变量
时,自变量 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年12月29日,国家发改委批复了昌景黄铁路项目可行性研究报告.该项目位于赣皖两省,线路起自江西省南昌市南昌东站,经上饶市、景德镇市,安徽省黄山市,终至黄山北站.按照设计,行驶180千米,昌景黄高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少20分钟,求昌景黄高铁列车的平均行驶速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知已知抛物线
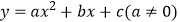 与x轴交于点
与x轴交于点 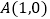 和点
和点 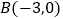 ,与y轴交于点C,且
,与y轴交于点C,且 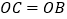 .
.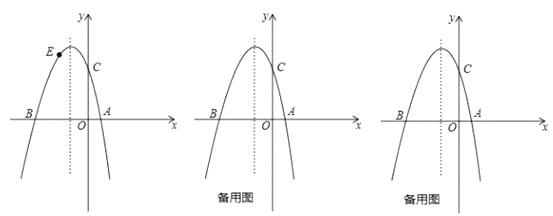
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
(4)连AC,H是抛物线上一动点,过点H作AC的平行线交x轴于点F,是否这样的点F,使得以A,C,H,F为顶点的四边形是平行四边形?若存在,直接写出满足条件的点F的坐标;若不存在,请说明理由.
相关试题

