【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
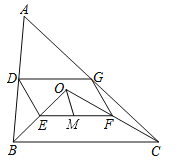
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
参考答案:
【答案】(1)证明见解析;(2)6.
【解析】试题分析:(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=![]() BC,DG∥BC且DG=
BC,DG∥BC且DG=![]() BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
(2)先判断出∠BOC=90°,再利用直角三角形斜边的中线等于斜边的一半,求出EF即可.
试题解析:(1)∵D、G分别是AB、AC的中点,∴DG∥BC,DG=![]() BC,∵E、F分别是OB、OC的中点,∴EF∥BC,EF=
BC,∵E、F分别是OB、OC的中点,∴EF∥BC,EF=![]() BC,∴DE=EF,DG∥EF,∴四边形DEFG是平行四边形;
BC,∴DE=EF,DG∥EF,∴四边形DEFG是平行四边形;
(2)∵∠OBC和∠OCB互余,∴∠OBC+∠OCB=90°,∴∠BOC=90°,∵M为EF的中点,OM=3,∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,∴DG=EF=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线MN与直线PQ相交于O,点A在射线OP上,点B在射线OM上.
(1)如图1,
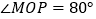 已知AG、BG分别是∠BAO和∠ABO角的平分线,求
已知AG、BG分别是∠BAO和∠ABO角的平分线,求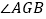 的度数;
的度数;(2)如图2,
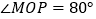 已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,∠CED= 度;
已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,∠CED= 度;(3)如图3,
 ,过点B作直线CD⊥MN,G为射线BD上一点,OF平分∠QOG,OE⊥OF,探索
,过点B作直线CD⊥MN,G为射线BD上一点,OF平分∠QOG,OE⊥OF,探索 的大小是否发生变化?若不变,求其值;若改变,说明理由.
的大小是否发生变化?若不变,求其值;若改变,说明理由.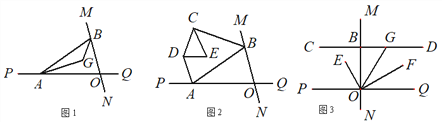
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图E在△ABC的边AC上,且∠AEB=∠ABC.
⑴求证:∠ABE=∠C;
⑵若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:
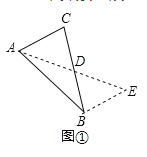

如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(x﹣3,x+3)是x轴上一点,则点P的坐标是( )
A.(0,6)B.(0,﹣6)C.(﹣6,0)D.(6,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把点A(3,5)向下平移3个单位长度,再向左平移2个单位长度后,得对应点A1的坐标是( )
A.(1,2)B.(2,1)C.(﹣1,2)D.(﹣1,﹣2)
相关试题

