【题目】如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正△ABC的边长为1,它的一边AC在MN上,且顶点A与M重合.现将正△ABC在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.
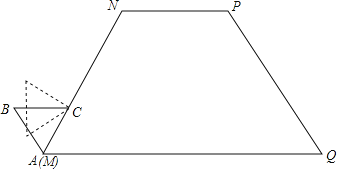
(1)请在所给的图中,画出顶点A在正△ABC整个翻滚过程中所经过的路线图;
(2)求正△ABC在整个翻滚过程中顶点A所经过的路径长;
(3)求正△ABC在整个翻滚过程中顶点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S.
参考答案:
【答案】(1)画图见解析;(2)点A所经过的路线长![]() π;(3)
π;(3)![]() π+
π+![]() .
.
【解析】
试题分析:(1)根据将正△ABC在梯形的外面沿边MN、NP、PQ进行翻滚翻滚到有一个顶点与Q重合即停止滚动,转动过程中始终是以半径为1的弧,据此画出圆弧即可.
(2)根据翻滚路线结合弧长公式求出即可;
(3)根据总结的翻转角度和翻转半径,求出圆弧与梯形的边长围成的扇形的面积即可.
解:(1)如图所示:
(2)点A所经过的路线长:![]() ×4+
×4+![]() =
=![]() π;
π;
(3)如图所示:

根据正三角形边长为1,则高AD为:cos30°=![]() ,则AD=
,则AD=![]() ,
,
故面积为:![]() ×1×
×1×![]() ,
,
围成的图形的面积:3个圆心角为120°的扇形+2个正三角形的面积+一个半圆面积,
(根据要求正△ABC在整个翻滚过程中顶点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S,则最后一段弧没有和PQ围成闭合的图形,故可以不求这部分面积)
所以点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S为:
![]() ×π×12+2×
×π×12+2×![]() 1×
1×![]() +3×
+3×![]() =
=![]() π+
π+![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2014次“移位”后,他到达编号为 的点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1) 填空:AB=_________,BC= ;
(2) 若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动.设运动时间为t秒,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,用含t的代数式表示BC和AB的长,并探索:BC-AB的值是否随着时间t的变化而改变?请说明理由
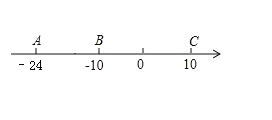
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
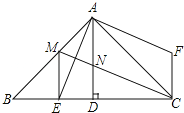
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.
求证:①ME⊥BC;②CM平分∠ACE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于E,DF⊥AC于点F.
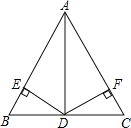
(1)请写出与A点有关的三个正确结论;
(2)DE与DF在数量上有何关系?并给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示0.000031,结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A,则此三角形( )
A. 一定有一个内角为45° B. 一定有一个内角为60°
C. 一定是直角三角形 D. 一定是钝角三角形
相关试题

