搜索
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的5个主题进行了抽样调查（每位同学只选取最关注的一个），根据调查结果绘制了两幅不完整的统计图，根据图中提供的信息，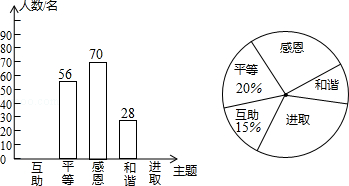
解答下列问题：
（1）这次调查的学生共有多少名？
（2）请将条形统计图补充完整；并写出这次主题班会调查结果的众数是；中位数落在的区域是 ．
（3）若该校学生人数为800人，请根据上述调查结果，估计该校学生中“感恩”的人数．
参考答案：
【答案】
（1）
解：56÷20%=280（名）；
答：这次调查的学生共有280名
（2）
；进取；平等
（3）
解：800×25%=200
答：该校学生中“感恩”的人数是200
【解析】解：（2）如图所示，280×15%=42（名），280﹣42﹣56﹣28﹣70=84（名），
故众数是：进取，中位数落在的区域是：平等；
故答案为：进取，感恩；
（1）根据“平等”的人数除以占的百分比得到调查的学生总数即可；（2）用总人数乘以每种情况所占的百分比后即可求得每一个小组的频数，从而补全统计图；（3）首先求得“感恩”的人数所占的百分比，然后确定“感恩”的人数学生数即可．
-
科目： 来源： 题型：
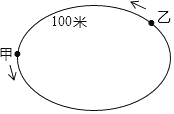
查看答案和解析>>【题目】已知甲沿周长为300米的环形跑道按逆时针方向跑步，速度为a米/秒，与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步，速度为3米/秒．
(1)若a＝1，求甲、乙两人第一次相遇所用的时间；
(2)若a＞3，甲、乙两人第一次相遇所用的时间为80秒，试求a的值．
-
科目： 来源： 题型：
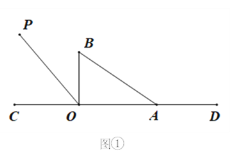
查看答案和解析>>【题目】如图①，直线CD上有一点O，过点O在直线CD上方作射线OP．将一直角三角尺AOB（∠AOB=90°）的直角顶点放在点O处，一条直角边OA在射线OD上，另一边OB在直线CD上方．将直角三角板绕着点O逆时针旋转．
(1)当直角三角板旋转到如图②的位置，OB恰好平分∠COP时，试证明：OA边恰好平分∠POD.
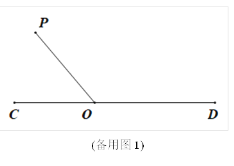
(2)若射线OP的位置保持不变，且∠COP=50°．当直角三角尺旋转到边AB与射线OC相交时则∠BOC与∠AOP有怎样的数量关系?试画出图形，写出数量关系，并写出说理过程.
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道：分式和分数有着很多的相似点．如类比分数的基本性质，我们得到了分式的基本性质；类比分数的运算法则，我们得到了分式的运算法则；等等．小学里，把分子比分母小的分数叫做真分数．类似地，我们把分子整式的次数小于分母整式的次数的分式称为真分式；反之，称为假分式．任何一个假分式都可以化成整式与真分式的和的形式，如：
； 
(1)下列分式中，属于真分式的是：________(填序号)；
①
②
③
④
(2)将假分式
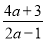化成整式与真分式的和的形式： 
＝________＋________；(3)将假分式
化成整式与真分式的和的形式： 
＝__________________. -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
在学习“分式方程及其解法”过程中，老师提出一个问题：若关于x的分式方程
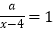的解为正数，求a的取值范围？经过独立思考与分析后，小明和小聪开始交流解题思路如下：
小明说：解这个关于x的分式方程，得到方程的解为
.由题意可得
，所以
，问题解决.小聪说：你考虑的不全面.还必须保证
才行.请回答：_______________的说法是正确的，并说明正确的理由是：__________________.
完成下列问题：
（1）已知关于x的方程
的解为非负数，求m的取值范围；（2）若关于x的分式方程
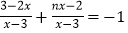无解.直接写出n的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点A、D在y轴正半轴上，点B、C分别在x轴上，CD平分∠ACB，与y轴交于D点，∠CAO=90°-∠BDO.
（1）求证：AC=BC：
（2）如图2，点C的坐标为（4，0），点E为AC上一点，且∠DEA=∠DBO，求BC+EC的长；
（3）如图3，过D作DF⊥AC于F点，点H为FC上一动点，点G为OC上一动点，当H在FC上移动、点G在OC上移动时，始终满足∠GDH=∠GDO+∠FDH，试判断FH、GH、OG这三者之间的数量关系，写出你的结论并加以证明.
（图3） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝AC，∠BAC＝40°，分别以AB，AC为边作两个等腰三角形ABD和ACE，且AB＝AD，AC＝AE，∠BAD＝∠CAE＝90°.
(1)求∠DBC的度数．
(2)求证：BD＝CE.
相关试题
