【题目】如图,在平面直角坐标系中,点A(-1,0),B(0,2),点C在x轴上,且∠ABC=90°.
(1)求点C的坐标;
(2)求经过A,B,C三点的抛物线的表达式;
(3)在(2)中的抛物线上是否存在点P,使∠PAC=∠BCO?若存在,求出点P的坐标;若不存在,说明理由.

参考答案:
【答案】(1)(4,0)(2)y=![]() ;(3)(3,2),(5,-3)
;(3)(3,2),(5,-3)
【解析】试题分析:(1)设点C 的坐标为(x,0),在直角三角形ABC中运用勾股定理即可求出x的值,从而确定点C的坐标;
(2)设出二次函数关系式,把A、B、C三点坐标代入求解即可;
(3) 存在,利用正切值相等,分两种情况列式计算即可.
试题解析:(1)设C(x,0)(x>0)
∴AC=x+1,BC=![]() ,AB=
,AB=![]()
∵∠ABC=90°
∴AB2+BC2=AC2
∴5+x2+4=(x+1)2
解得:x=4
∴C(4,0)
(2)∵A(-1,0),B(0,2),C(4,0)
设抛物线的解析式为:y=a(x+1)(x-4)
把点B(0,2)代入上式得:a=![]()
∴抛物线的解析式为:y=![]() (x+1)(x-4)=
(x+1)(x-4)= ![]() x2+
x2+![]() x+2;
x+2;
(3)∵∠PAC=∠BCO
∴tan∠PAC=tan∠BCO
∴tan∠PAC=tan∠BCO=![]()
设P点坐标为(x,y)
当点P在x轴上方时,y>0
∴tan∠PAC=![]()
联立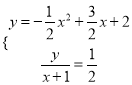
∴x2-2x-3=0
∵y>0
∴x=3
∴点P坐标为(3,2)
当点P在x轴下方时,y<0,x>0
∴tan∠PAC=![]()
联立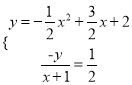
∴x2-4x-5=0
∵y<0
∴x=-5
∴点P坐标为(-5,3)
综上可得:点P的坐标为(3,2)或(-5,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
 中,
中,  ,
,  ,点
,点 是
是 的中点,点
的中点,点 是边
是边 上一点.
上一点.(
 )如图
)如图 ,若
,若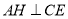 交
交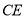 延长线于点
延长线于点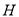 ,交
,交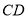 的延长线于点
的延长线于点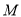 ,求证:
,求证: 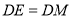 ;
;(
 )如图
)如图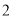 ,若
,若 为线段
为线段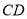 上一点,且
上一点,且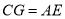 ,
, 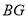 的延长线交
的延长线交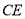 于
于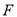 ,请判断线段
,请判断线段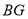 与
与 的关系,并证明你的猜想.
的关系,并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(3,n)在二次函数y=x2+2x﹣3的图象上,则n的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在半径为4厘米的圆面中,挖去一个半径为x厘米的圆面,剩下部分的面积为y平方厘米,写出y关于x的函数解析式:(结果保留π,不要求写出定义域)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒2个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
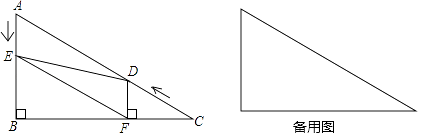
(1)求证:AE=DF;
(2)当四边形BFDE是矩形时,求t的值;
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.
(1)说明方程x2-3x+2=0是倍根方程;
(2)说明:若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;
(3)如果方程ax2+bx+c=0是倍根方程,且相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,试说明方程ax2+bx+c=0的一个根为
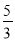 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,根据图中数据完成填空,再按要求答题:

(1)sin2A1+sin2B1= . sin2A2+sin2B2= .sin2A3+sin2B3= ;
(2)观察上述等式,猜想在Rt△ABC中,∠C=90°,都有sin2A+sin2B= ;
(3)如图④,在Rt△ABC中,∠C=90°,∠A、∠B、 ∠C 的对边分别是a、b、c,利用三角函数的定义和勾股定理,证明你的猜想;
(4)已知∠A+∠B =90°且sinA=
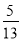 ,求sinB.
,求sinB.
相关试题

