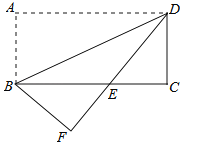
【题目】(2016四川省乐山市第20题)如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
参考答案:
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题分析:(1)由AD∥BC,知∠ADB=∠DBC,根据折叠的性质∠ADB=∠BDF,所以∠DBC=∠BDF,得BE=DE,即可用AAS证△DCE≌△BFE;
(2)在Rt△BCD中,CD=2,∠ADB=∠DBC=30°,知BC=![]() ,在Rt△BCD中,CD=2,∠EDC=30°,知CE=
,在Rt△BCD中,CD=2,∠EDC=30°,知CE=![]() ,所以BE=BC﹣EC=
,所以BE=BC﹣EC=![]() .
.
试题解析:(1)∵AD∥BC,∴∠ADB=∠DBC,根据折叠的性质∠ADB=∠BDF,∠F=∠A=∠C=90°,∴∠DBC=∠BDF,∴BE=DE,在△DCE和△BFE中,∵∠BEF=∠DEC,∠F=∠C,BE=DE,∴△DCE≌△BFE;
(2)在Rt△BCD中,∵CD=2,∠ADB=∠DBC=30°,∴BC=![]() ,在Rt△BCD中,∵CD=2,∠EDC=30°,∴DE=2EC,∴
,在Rt△BCD中,∵CD=2,∠EDC=30°,∴DE=2EC,∴![]() ,∴CE=
,∴CE=![]() ,∴BE=BC﹣EC=
,∴BE=BC﹣EC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中有一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线。
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线;
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数;
(3)如图2,△ABC中,AC=2,BC=
 ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长。
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长。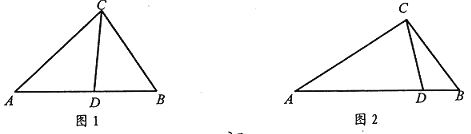
-
科目: 来源: 题型:
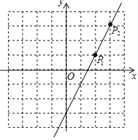
查看答案和解析>>【题目】如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.
(1)求直线l所表示的一次函数的表达式;
(2)若将点P2先向右平移3个单位,再向上平移6个单位得到像点P3.请判断点P3是否在直线l上,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是( )
A.锐角三角形B.直角三角形C.钝角三角形D.任意三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△DEF,△ABC的面积为1,△DEF的面积为4,则△ABC与△DEF的周长之比为( )
A. 1∶2 B. 1∶4 C. 2∶1 D. 4∶1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
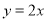 与反比例函数
与反比例函数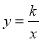 的图像交于点
的图像交于点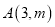 ,点
,点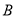 是线段
是线段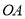 的中点,点
的中点,点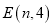 在反比例函数的图像上,点
在反比例函数的图像上,点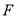 在
在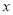 轴上,若
轴上,若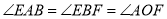 ,则点
,则点 的横坐标为__________.
的横坐标为__________.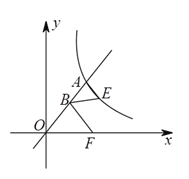
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面内两点M、N,如果它们平移的方式相同,那么平移后它们之间的相对位置是( )
A.不能确定
B.发生变化
C.不发生变化
D.需分情况说明
相关试题

