【题目】如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,若把直角三角形绕边AB所在直线旋转一周,则所得几何体的表面积为 . 
参考答案:
【答案】![]()
【解析】解:∵Rt△ABC中,∠ACB=90°,AC=4,BC=3, ∴AB= ![]() =5,
=5,
设AB边上的高为h,则 ![]() ×5h=
×5h= ![]() ×3×4,
×3×4,
解得:h= ![]() ,
,
∴所得两个圆锥底面半径为 ![]() ,
,
∴几何体的表面积= ![]() ×2π×
×2π× ![]() ×4+
×4+ ![]() ×2π×
×2π× ![]() ×3=
×3= ![]() π.
π.
则所得几何体的表面积为 ![]() .
.
【考点精析】掌握点、线、面、体的认识和圆锥的相关计算是解答本题的根本,需要知道点:线和线相交的地方是点,它是几何图形中最基本的图形;线:面和面相交的地方是线,分为直线和曲线;面:包围着体的是面,分为平面和曲面;体:几何体也简称体;圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h..
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠C=90°,BC=3,D,E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )

A.
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )

A.3次
B.4次
C.5次
D.6次 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是边BC上的点,分别连结AE、BD相交于点O,若AD=5,
 =
=  ,则EC= .
,则EC= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N= .
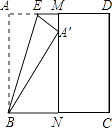
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.

(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接河南省第30届青少年科技创新大赛,某中学向七年级学生征集科幻画作品,李老师从七年级12个班中随机抽取了A、B、C、D四个班,对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图(如图)

(1)李老师所调查的4个班征集到作品共件,其中B班征集到作品 , 请把图补充完整;
(2)李老师所调查的四个班平均每个班征集到作品多少件?请估计全年级共征集到作品多少件?
(3)如果全年级参展作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生.现在要抽两人去参加学校总结表彰座谈会,用树状图或列表法求出恰好抽中一男一女的概率.
相关试题

