【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.

(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
参考答案:
【答案】证明见解析;(2)GE垂直平分DF.
【解析】
试题分析:(1)由AD与BC平行,利用两直线平行内错角相等,得到一对角相等,再由一对对顶角相等及E为AB中点得到一对边相等,利用AAS即可得出△ADE≌△BFE;
(2)∠GDF=∠ADE,以及(1)得出的∠ADE=∠BFE,等量代换得到∠GDF=∠BFE,利用等角对等边得到GF=GD,即三角形GDF为等腰三角形,再由(1)得到DE=FE,即GE为底边上的中线,利用三线合一即可得到GE与DF垂直.
试题解析:(1)证明:∵AD∥BC,∴∠ADE=∠BFE,
∵E为AB的中点,∴AE=BE,
在△AED和△BFE中,
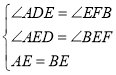
∴△AED≌△BFE(AAS);
(2)解:EG与DF的位置关系是EG垂直平分DF,
理由为:连接EG,
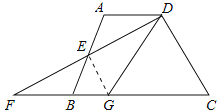
∵∠GDF=∠ADE,∠ADE=∠BFE,
∴∠GDF=∠BFE,
由(1)△AED≌△BFE得:DE=EF,即GE为DF上的中线,
∴GE垂直平分DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB⊥BC,CD⊥BC,垂足分别为B、C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为( )

A. 4cm B. 8cm C. 9cm D. 10cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P的坐标为(a+1,2a-7),且点P到两坐标轴的距离相等,则点P的坐标是( )
A.(3,3)B.(3,-3)C.(9,9)D.(3,-3)或(9,9)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:8a3÷(﹣2a)=_____.
-
科目: 来源: 题型:
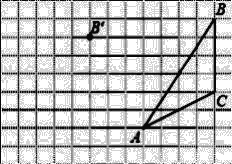
查看答案和解析>>【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和直尺,完成下列各题:
(1)补全△A′B′C′;
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)点Q为格点(点Q不与点B重合),且△ACQ的面积等于△ABC的面积,Q点有____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(3,2),AC⊥x轴,垂足为点C,则点C的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,码头A、B分别在海岛O的北偏东45°和北偏东60°方向上,仓库C在海岛O的北偏东75°方向上,码头A、B均在仓库C的正西方向,码头B和仓库C的距离BC=50km,若将一批物资从仓库C用汽车运送到A、B两个码头中的一处,再用货船运送到海岛O,若汽车的行驶速度为50km/h,货船航行的速度为25km/h,问这批物资在哪个码头装船,最早运抵海岛O?(两个码头物资装船所用的时间相同,参考数据:
 ≈1.4,
≈1.4,  ≈1.7)
≈1.7)
相关试题

