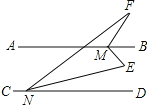
【题目】如图所示,直线AB∥CD,NE平分∠FND,MB平分∠FME,且2∠E+∠F=222°,则∠FME的度数是_____.
参考答案:
【答案】148°.
【解析】
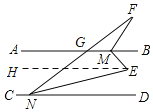
过点E作EH∥AB,根据平行于同一条直线的两直线平行,可得AB∥CD∥EH,设∠BME=α,∠END=β,利用平行线的性质和角平分线的定义即可列出关于α的方程,从而求出∠FME的度数.
解:过点E作EH∥AB,
∵AB∥CD,
∴AB∥CD∥EH,
设∠BME=α,∠END=β,
∴∠MEH=∠BME=α,∠NEH=∠END=β,
∴∠MEN=α+β,
∵NE平分∠FND,MB平分∠FME,
∴∠BMF=α,∠FND=2β,
∵AB∥CD,
∴∠FGB=2β,
∵∠BMF=∠FGB+∠F,
∴α=2β+∠F,
∴3α=2α+2β+∠F,
∴3α=2(α+β)+∠F,
∴3α=2∠MEN+∠F=222°,
∴α=74°,
∴∠FME=2α=148°,
故答案为:148°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,
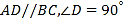 ,E为边BC上一点,且EC=AD,连接AC.
,E为边BC上一点,且EC=AD,连接AC.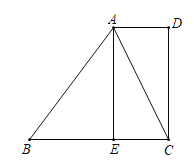
(1)求证:四边形AECD是矩形;
(2)若AC平分∠DAB,AB=5,EC=2,求AE的长, -
科目: 来源: 题型:
查看答案和解析>>【题目】中国新版高铁“复兴号”率先在北京南站和上海虹桥站双向首发“复兴号”高铁从某车站出发,在行驶过程中速度
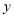 (千米/分钟)与时间
(千米/分钟)与时间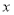 (分钟)的函数关系如图所示.
(分钟)的函数关系如图所示.
(1)当
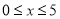 时,求
时,求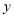 关于
关于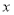 工的函数表达式,
工的函数表达式,(2)求点
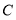 的坐标.
的坐标. (3)求高铁在
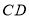 时间段行驶的路程.
时间段行驶的路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(+12)﹣(﹣7)+(﹣5)﹣(+30)
(2)
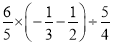
(3)﹣33×(﹣2)﹣12÷[(﹣3)﹣(﹣1)]
(4)(﹣
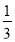 )×(﹣3)3﹣0.25×(﹣3)×(﹣2)4
)×(﹣3)3﹣0.25×(﹣3)×(﹣2)4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠ABC=45°.点D在AB上,点E在BC上,且AE⊥CD,若AE=CD,BE:CE=5:6,S△BDE=75,则S△ABC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知a2+b2=10,a+b=4,求a﹣b的值;
(2)关于x的代数式(ax﹣3)(2x+1)﹣4x2+m化简后不含有x2项和常数项,且an+mn=1,求2n3﹣9n2+8n+2019的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习反比例函数的图像时,他的老师要求同学们根据“探索一次函数
 的图像”的基本步骤,在纸上逐步探索函数
的图像”的基本步骤,在纸上逐步探索函数 的图像,并且在黑板上写出4个点的坐标:
的图像,并且在黑板上写出4个点的坐标:  ,
,  ,
,  ,
,  .
.⑴ 在A、B、C、D四个点中,任取一个点,这个点既在直线
 又在双曲线
又在双曲线 上的概率是多少?
上的概率是多少?⑵ 小明从A、B、C、D四个点中任取两个点进行描点,求两点都落在双曲线
 上的概率.
上的概率.
相关试题

