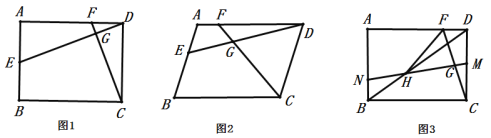
【题目】菱形![]() 中,
中,![]() 为边
为边![]() 上的点,
上的点,![]() 相交于点
相交于点![]() .
.
(1)如图1,若![]() ,
,![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() .求证:
.求证:![]() ;
;
(3)如图3,在(1)的条件下,平移线段![]() 到
到![]() ,使
,使![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
参考答案:
【答案】(1)见解析;(2)见解析;(3)1+![]() .
.
【解析】
(1)由菱形ABCD中和∠A=90°可得菱形ABCD是正方形,根据正方形性质得AD=DC,∠A=∠CDF=90°,再加上DE=CF即证得Rt△ADE≌Rt△DCF,所以∠ADE=∠DCF,等量代换计算即得到∠CGD=90°,得证.
(2)由菱形性质可得AD=CD,∠B=∠ADC,∠B+∠BAD=180°,再由∠EGC+∠B=180°可得∠A=∠EGC=∠DGF,∠CGD=∠B=∠ADC,证明△ADE∽△GDF和△DCG∽△FCD,再由对应边成比例等量代换计算得DE=CF.
(3)由(1)的条件可得MN=CF,MN⊥CF,加上G为CF的中点,即MN垂直平分CF,连接FM即有FM=MC且∠DMF=∠MFC+∠FCD=30°,设DF=x,则根据30°直角三角形的性质,可用x表示FM、DM.过点N作CD的垂线段NP,则CP=BN=![]() ,且易证Rt△NPM≌Rt△CDF,所以MP=DF=x,进而能用x表示CM、CD.利用MF=MC列出关于x的方程,求解即得到CM、CD、DF的长.证明△CGM∽△CDF,根据对应边成比例计算即求得FG=CG的长.
,且易证Rt△NPM≌Rt△CDF,所以MP=DF=x,进而能用x表示CM、CD.利用MF=MC列出关于x的方程,求解即得到CM、CD、DF的长.证明△CGM∽△CDF,根据对应边成比例计算即求得FG=CG的长.
解:(1)证明:∵菱形ABCD中,∠A=90°
∴菱形ABCD是正方形
∴AD=DC,∠A=∠CDF=90°
在Rt△ADE与Rt△DCF中
DE=CF,AD=DC,
∴Rt△ADE≌Rt△DCF(HL)
∴∠ADE=∠DCF
∴∠DCF+∠CDE=∠ADE+∠CDE=∠ADC=90°
∴∠CGD=90°
∴DE⊥CF
(2)证明:∵四边形ABCD是菱形
∴AD=CD,∠B=∠ADC,AD∥BC
∴∠A+∠B=180°
∵∠EGC+∠B=180°,∠EGC+∠CGD=180°
∴∠A=∠EGC=∠DGF,∠CGD=∠B=∠ADC
∵∠A=∠DGF,∠ADE=∠GDF
∴△ADE∽△GDF
∴![]() ,
,
∴![]()
∵∠CGD=∠CDF,∠DCG=∠FCD
∴△DCG∽△FCD
∴![]() ,
,
∴![]() ,
,
∵AD=DC,
∴DE=CF;
(3)如图,过点N作NP⊥CD于点P,连接FM,
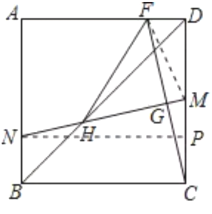
∴∠CPN=∠MPN=90°,
∵四边形ABCD是正方形
∴∠ABC=∠BCD=∠ADC=90°,BC=CD
∴四边形BCPN是矩形
∴NP=BC=CD,PC=BN=![]() ,
,
在Rt△NPM与Rt△CDF中
MN=CF,NP=CD,
∴Rt△NPM≌Rt△CDF(HL)
∴PM=DF
设PM=DF=x,则CM=PC+PM=![]() +x,
+x,
∵由(1)得MN⊥CF,G为CF中点
∴MN垂直平分CF
∴MF=MC
∴∠MFC=∠FCD=15°
∴∠DMF=∠MFC+∠FCD=30°
∴Rt△DMF中,MF=2DF=2x,DM=![]() ,
,
由于MF=MC,即2x=![]() +x
+x
∴x=![]()
∴DF=![]() ,DM=
,DM=![]() ,CM=MF=2
,CM=MF=2![]() ,CD=CM+DM=2
,CD=CM+DM=2![]() +
+![]()
∵∠GCM=∠MCF,∠CGM=∠CDF=90°
∴△CGM∽△CDF
∴![]() ,
,
∴2CG2=CDCM=(2![]() +
+![]() )2
)2![]() =8+4
=8+4![]() ,
,
∴CG2=4+2![]() =12+2
=12+2![]() +(
+(![]() )2=(1+
)2=(1+![]() )2,
)2,
∴FG=CG=1+![]() .
.
-
科目: 来源: 题型:
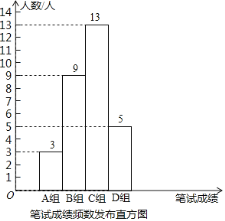
查看答案和解析>>【题目】某公司为了到高校招聘大学生,为此设置了三项测试:笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3:2:5的比例确定.公司初选了若干名大学生参加笔试,面试,并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息:
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
平均数
中位数
众数
最高分
笔试成绩
81
m
92
97
面试成绩
80.5
84
86
92
根据以上信息,回答下列问题:
(1)这批大学生中笔试成绩不低于88分的人数所占百分比为 .
(2)m= 分,若甲同学参加了本次招聘,他的笔试、面试成绩都是83分,那么该同学成绩排名靠前的是 成绩,理由是 .
(3)乙同学也参加了本次招聘,笔试成绩虽不是最高分,但也不错,分数在D组;面试成绩为88分,实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分;若该公司最终录用的最低分数线为86分,请通过计算说明,该同学最终能否被录用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在
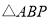 中,
中, 是
是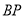 边上一点,
边上一点,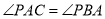 ,
,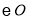 是
是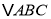 的外接圆,
的外接圆,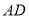 是
是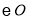 的直径,且交
的直径,且交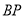 于点
于点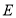 .
.(1)求证:
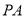 是
是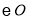 的切线;
的切线;(2)过点
 作
作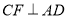 ,垂足为点
,垂足为点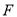 ,延长
,延长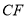 交
交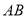 于点
于点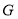 ,若
,若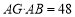 ,求
,求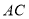 的长;
的长;(3)在满足(2)的条件下,若
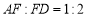 ,
,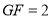 ,求
,求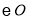 的半径及
的半径及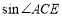 的值.
的值.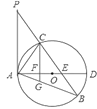
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市“上品”房地产开发公司于2010年5月份完工一商品房小区,6月初开始销售,其中6月的销售单价为0.7万元
 ,7月的销售单价为0.72万元
,7月的销售单价为0.72万元 ,且每月销售价格
,且每月销售价格 (单位:万元
(单位:万元 )与月份
)与月份 (
(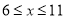 ,
,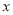 为整数)之间满足一次函数关系:每月的销售面积为
为整数)之间满足一次函数关系:每月的销售面积为 (单位:
(单位: ),其中
),其中 .(
.(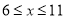 ,
,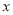 为整数).
为整数).(1)求
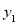 与月份
与月份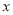 的函数关系式;
的函数关系式;(2)6~11月中,哪一个月的销售额最高?最高销售额为多少万元?
(3)2010年11月时,因会受到即将实行的“国八条”和房产税政策的影响,该公司销售部预计12月份的销售面积会在11月销售面积基础上减少
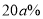 ,于是决定将12月份的销售价格在11月的基础上增加
,于是决定将12月份的销售价格在11月的基础上增加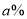 ,该计划顺利完成.为了尽快收回资金,2011年月公司进行降价促销,该月销售额为
,该计划顺利完成.为了尽快收回资金,2011年月公司进行降价促销,该月销售额为 万元.这样12月、1月的销售额共为4618.4万元,请根据以上条件求出
万元.这样12月、1月的销售额共为4618.4万元,请根据以上条件求出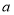 的值为多少?
的值为多少? -
科目: 来源: 题型:
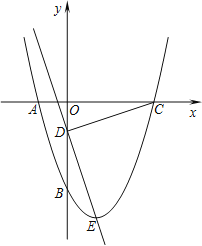
查看答案和解析>>【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B是反比例函数y=
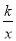 (k≠0)图象上的两点,延长线段AB交y轴于点C,且点B为线段AC中点,过点A作AD⊥x轴于点D,点E为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )
(k≠0)图象上的两点,延长线段AB交y轴于点C,且点B为线段AC中点,过点A作AD⊥x轴于点D,点E为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )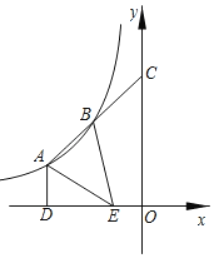
A.﹣12B.﹣10C.﹣9D.﹣6
-
科目: 来源: 题型:
查看答案和解析>>【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A.
 B.
B. 
C.
 D.
D. 
相关试题

