【题目】在同一平面内的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离“,记作d(M,N).
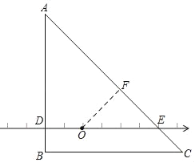
如图,等腰直角三角形ABC的一条直角边AB垂直数轴于点D,斜边AC与数轴交于点E,数轴上点O表示的有理数是0,若AB=BC=8,AD=6,OD=2.点O到边BC的距离与线段DB的长相等.
(1)求d(点O,点E);
(2)求d(点O,△ABC).
参考答案:
【答案】(1)4;(2)2.
【解析】
(1)根据等腰直角三角形的性质和线段的和差关系求得OE=4.再根据“闭距离”的定义可得d(点O,点E)=4.
(2)过点O作OF⊥AC于点F,可得OF=FE,设OF=FE=x,在Rt△OEF中,可求点O到边AC距离OF是2![]() ,进一步得到对于△ABC三边上任意一点Q,O,Q两点间的距离的最小值为2.再根据“闭距离”的定义可得d(点O,△ABC)=2.
,进一步得到对于△ABC三边上任意一点Q,O,Q两点间的距离的最小值为2.再根据“闭距离”的定义可得d(点O,△ABC)=2.
解:(1)∵等腰直角三角形ABC,AB=BC=8,
∴∠C=∠A=45°
∠ABC=90°.
∵AB垂直数轴于点D,
∴∠ADE=∠ABC=90°.
∴BC∥DE
∴∠AED=∠C=∠A=45°.
∴AD=DE.
∵AD=6,
∴DE=AD=6,
∵OD=2,
∴OE=4.
∴d(点O,点E)=4.
(2)过点O作OF⊥AC于点F,
∵∠AED=45°,OE=4,
∴∠AED=∠FOE=45°
∴OF=FE,
设OF=FE=x,
在Rt△OEF中,x2+x2=16x2=8,![]() (负值舍去),
(负值舍去),
![]() ,
,
∴点O到边AC距离OF是![]() ,
,
∵AB=8,AD=6,
∴DB=AB﹣AD=2.
∵点O到边BC的距离与线段DB的长相等.
∴点O到边BC距离是2,
∵点O到边AB距离OD是2,
∴对于△ABC三边上任意一点Q,O,Q两点间的距离的最小值为2.
∴d(点O,△ABC)=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索研究:已知:△ABC和△CDE都是等边三角形.
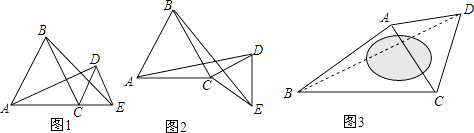
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为: ,
线段AD与BE所成的锐角度数为°;
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.

(1)如图1,若四边形ABCD是正方形.请直接写出AC1 与BD1的数量关系和位置关系.
(2)如图2,若四边形ABCD是菱形,AC=6,BD=8,判断AC1与BD1的数量关系和位置关系,并给出证明;
(3)如图3,若四边形ABCD是平行四边形,AC=6,BD=12,连接DD1 , 设AC1=kBD1 , 请直接写出k的值和AC12+(kDD1)2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小晶设计的“作互相垂直的两条直线”的尺规作图过程.
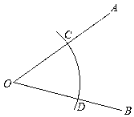
作法:如图,
①在平面内任选一点O,作射线OA,OB;
②以O为圆心,以任意长为半径作弧,分别交OA于点C,交OB于点D;
③分别以C,D为圆心,以大于
 CD的同样长为半径作弧,两弧交于∠AOB内部一点P;
CD的同样长为半径作弧,两弧交于∠AOB内部一点P;④连接CP、PD;
⑤作直线OP,作直线CD,两直线相交于点E;则直线CD与OP就是所求作的互相垂直的两条直线.根据小晶设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OC= ,CP= ,OP=OP
∴△OPC≌△OPD
∴∠AOP=∠BOP.
∴OE是△COD的高线( )(填推理的依据)
即OE⊥CD.
∴CD与OP互相垂直
-
科目: 来源: 题型:
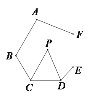
查看答案和解析>>【题目】如图,在六边形ABCDEF中,∠A+∠B+∠E+∠F=α,CP、DP分别平分∠BCD、∠CDE,则∠P的度数是( )
A.
 α-180°B. 180°-
α-180°B. 180°- C.
C.  D. 360°-
D. 360°-
-
科目: 来源: 题型:
查看答案和解析>>【题目】某营业厅对手机话费业务有如下的优惠:
优惠规则:
①用户手机账户原有话费不能低于240元;
②办理业务时,首先从手机账户中一次性扣除240元,并把这240元抵为300元话费,然后将这300元话费分12次,在每月的15号等额返还到手机账户;
③每月1号从手机账户中扣除话费49元,当月不再扣除其他任何费用;
④每月1号手机账户的话费余额不足以扣除49元时,视为欠费,则当月不再返还等额的话费.
小明的手机账户中原有话费400元,办理了这项优惠业务,设小明的手机账户中每个月末的话费余额是y(元),月数为x(个),则
(1)每个月等额返还的话费是元,第2个月末的话费余额是元;
(2)求y关于x的函数关系式;
(3)若不续费,小明的手机第几个月会欠费? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
相关试题

