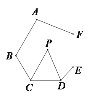
【题目】如图,在六边形ABCDEF中,∠A+∠B+∠E+∠F=α,CP、DP分别平分∠BCD、∠CDE,则∠P的度数是( )
A. ![]() α-180°B. 180°-
α-180°B. 180°-![]() C.
C. ![]() D. 360°-
D. 360°-![]()
参考答案:
【答案】A
【解析】
根据六边形的内角和公式表示出∠EDC+∠BCD,然后根据角平分线的定义可得∠PDC=![]() ∠EDC,∠PCD=
∠EDC,∠PCD=![]() ∠BCD,然后根据三角形内角和定理列式整理即可得解.
∠BCD,然后根据三角形内角和定理列式整理即可得解.
解:六边形ABCDEF的内角和为:(6-2)180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=![]() ∠EDC,∠PCD=
∠EDC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠P=180°-∠PDC-∠PCD
=180°-![]() ∠EDC-
∠EDC-![]() ∠BCD
∠BCD
=180°-![]() (∠EDC+∠BCD)
(∠EDC+∠BCD)
=180°-![]() (720°-∠A-∠B-∠E-∠F)
(720°-∠A-∠B-∠E-∠F)
=![]() (∠A+∠B+∠E+∠F)-180°,
(∠A+∠B+∠E+∠F)-180°,
即∠P=![]() (∠A+∠B+∠E+∠F)-180°.又∵∠A+∠B+∠E+∠F=α,
(∠A+∠B+∠E+∠F)-180°.又∵∠A+∠B+∠E+∠F=α,
故答案为:∠P=![]() α-180°.
α-180°.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.

(1)如图1,若四边形ABCD是正方形.请直接写出AC1 与BD1的数量关系和位置关系.
(2)如图2,若四边形ABCD是菱形,AC=6,BD=8,判断AC1与BD1的数量关系和位置关系,并给出证明;
(3)如图3,若四边形ABCD是平行四边形,AC=6,BD=12,连接DD1 , 设AC1=kBD1 , 请直接写出k的值和AC12+(kDD1)2的值. -
科目: 来源: 题型:
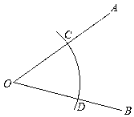
查看答案和解析>>【题目】下面是小晶设计的“作互相垂直的两条直线”的尺规作图过程.
作法:如图,
①在平面内任选一点O,作射线OA,OB;
②以O为圆心,以任意长为半径作弧,分别交OA于点C,交OB于点D;
③分别以C,D为圆心,以大于
 CD的同样长为半径作弧,两弧交于∠AOB内部一点P;
CD的同样长为半径作弧,两弧交于∠AOB内部一点P;④连接CP、PD;
⑤作直线OP,作直线CD,两直线相交于点E;则直线CD与OP就是所求作的互相垂直的两条直线.根据小晶设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OC= ,CP= ,OP=OP
∴△OPC≌△OPD
∴∠AOP=∠BOP.
∴OE是△COD的高线( )(填推理的依据)
即OE⊥CD.
∴CD与OP互相垂直
-
科目: 来源: 题型:
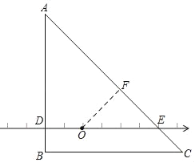
查看答案和解析>>【题目】在同一平面内的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离“,记作d(M,N).
如图,等腰直角三角形ABC的一条直角边AB垂直数轴于点D,斜边AC与数轴交于点E,数轴上点O表示的有理数是0,若AB=BC=8,AD=6,OD=2.点O到边BC的距离与线段DB的长相等.
(1)求d(点O,点E);
(2)求d(点O,△ABC).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某营业厅对手机话费业务有如下的优惠:
优惠规则:
①用户手机账户原有话费不能低于240元;
②办理业务时,首先从手机账户中一次性扣除240元,并把这240元抵为300元话费,然后将这300元话费分12次,在每月的15号等额返还到手机账户;
③每月1号从手机账户中扣除话费49元,当月不再扣除其他任何费用;
④每月1号手机账户的话费余额不足以扣除49元时,视为欠费,则当月不再返还等额的话费.
小明的手机账户中原有话费400元,办理了这项优惠业务,设小明的手机账户中每个月末的话费余额是y(元),月数为x(个),则
(1)每个月等额返还的话费是元,第2个月末的话费余额是元;
(2)求y关于x的函数关系式;
(3)若不续费,小明的手机第几个月会欠费? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,是一个长为 2m,宽为 2n 的长方形,沿图中虚线用剪刀将其均分成四个完全相同的小长方形,然后按图 2 的形状拼图.
(1)图 2 中的图形阴影部分的边长为 ;(用含 m、n 的代数式表示)
(2)请你用两种不同的方法分别求图 2 中阴影部分的面积; 方法一: ;方法二: .
(3)观察图 2,请写出代数式(m+n)2、(m﹣n)2、4mn 之间的关系式: .

相关试题

