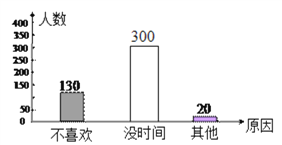
【题目】为了开展阳光体育运动,某市教体局做了一个随机调查,调查内容是:每天锻炼是否超过1h及锻炼未超过1h的原因.他们随机调查了600名学生,用所得的数据制成了扇形统计图和频数分布直方图(图1、图2).

根据图示,请回答以下问题:
(1)“没时间”的人数是 ,并补全频数分布直方图;
(2)2016年该市中小学生约40万人,按此调查,可以估计2016年全市中小学生每天锻炼超过1h的约有 万人;
(3)在(2)的条件下,如果计划2018年该市中小学生每天锻炼未超过1h的人数降到7.5万人,求2016年至2018年锻炼未超过1h人数的年平均降低的百分率.
参考答案:
【答案】(1)300 (2)10 (3)50%
【解析】试题分析:
(1)由扇形统计图中的信息可得被调查的600人中,锻炼不超过1h的人有450人,结合频数直方图中的信息即可得到“没有时间”的人数为300人,由此即可补全频数直方图;
(2)由扇形统计图可知,每天锻炼超过1h的约为![]() ,由此估计出全市中小学生每天锻炼超过1h的人数为40×
,由此估计出全市中小学生每天锻炼超过1h的人数为40×![]() =10(万人);
=10(万人);
(3)由(2)中结果可知,每天锻炼不超过1h小时的中小学生约有30万人,设平均每年降低的百分率为x,则由题意可得![]() ,解方程,并结合实际意义检验即可得到所求的百分率.
,解方程,并结合实际意义检验即可得到所求的百分率.
试题解析:
(1)由两幅统计图中的信息可得: ![]() (人),即每天锻炼不超过1h的人属于“没时间”的有300人,由此补充完整频数直方图如下:
(人),即每天锻炼不超过1h的人属于“没时间”的有300人,由此补充完整频数直方图如下:
(2)由题意可得:40×![]() =10(万人),即全市中小学生每天锻炼超过1h的约有10万人;
=10(万人),即全市中小学生每天锻炼超过1h的约有10万人;
(3)设平均每年降低的百分率为x,则由题意可得:
![]() ,解得:
,解得: ![]() (不合题意,舍去),
(不合题意,舍去),
∴年平均降低的百分率为50%.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”的
对于图形
 和图形
和图形 ,若图形
,若图形 和图形
和图形 分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形
分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形 和图形
和图形 是“中心轴对称”的。
是“中心轴对称”的。特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的。
(1)如图1,在正方形ABCD中,点
 ,点
,点 ,
,①下列四个点
 ,
, ,
, ,
, 中,与点A是“中心轴对称”的是________;
中,与点A是“中心轴对称”的是________;②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标
 的取值范围;
的取值范围;(2)四边形GHJK的四个顶点的坐标分别为
 ,
, ,
, ,
, ,一次函数
,一次函数 图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。
图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有A、B两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室阅读.
(1)下列事件中,是必然事件的为( )
A.甲、乙同学都在A阅览室 B.甲、乙、丙同学中至少两人在A阅览室
C.甲、乙同学在同一阅览室 D.甲、乙、丙同学中至少两人在同一阅览室
(2)用画树状图的方法求甲、乙、丙三名学生在同一阅览室阅读的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用长度相等的小棒按一定规律摆成的一组图案
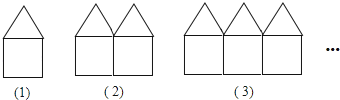
(1)填写下表:
图形序号
①
②
③
……
⑧
每个图案中小棒的数量
6
11
……
(2)请填写出第
 个图案中小棒的数量(用含
个图案中小棒的数量(用含 的代数式表示);
的代数式表示);(3)第30个图案中小棒有多少根?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,有两个点
 ,
, .
.(1)若
 、
、 关于
关于 轴对称,则
轴对称,则 _________________,
_________________, ________________.
________________.(2)若
 、
、 关于
关于 轴对称,则
轴对称,则 _________________,
_________________, ________________.
________________.(3)若
 、
、 两点重合,将重合后的点绕原点顺时针旋转
两点重合,将重合后的点绕原点顺时针旋转 ,此时点的坐标为__________.
,此时点的坐标为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 .
.(1)
 为何值时,
为何值时, 随
随 的增大而减小?
的增大而减小?(2)
 为何值时,函数图象与
为何值时,函数图象与 轴的交点在
轴的交点在 轴下方?
轴下方?(3)
 ,
, 分别是何值时,函数图象经过原点?
分别是何值时,函数图象经过原点?(4)当
 ,
, 时,求这个一次函数的图象与两个坐标轴的交点.
时,求这个一次函数的图象与两个坐标轴的交点.
相关试题

