【题目】平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”的
对于图形![]() 和图形
和图形![]() ,若图形
,若图形![]() 和图形
和图形![]() 分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形
分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形![]() 和图形
和图形![]() 是“中心轴对称”的。
是“中心轴对称”的。
特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的。
(1)如图1,在正方形ABCD中,点![]() ,点
,点![]() ,
,
①下列四个点![]() ,
,![]() ,
,![]() ,
,![]() 中,与点A是“中心轴对称”的是________;
中,与点A是“中心轴对称”的是________;
②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标![]() 的取值范围;
的取值范围;
(2)四边形GHJK的四个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,一次函数
,一次函数![]() 图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。
图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。

参考答案:
【答案】(1)①P1,P4;②![]() ≤xE≤
≤xE≤![]() ;(2)2
;(2)2![]() ≤b≤2+2
≤b≤2+2![]() 或-2-2
或-2-2![]() ≤b≤-2
≤b≤-2![]() .
.
【解析】
(1)①根据画出图形,根据“中心轴对称”的定义即可判断.
②以O为圆心,OA为半径画弧交射线OB于E,以O为圆心,OC为半径画弧交射线OB于F.求出点E,点F的坐标即可判断.
(2)如图3中,设GK交x轴于P.求出两种特殊位置的b的值即可判断:当一次函数y=![]() x+b经过点G(-2,2)时,2=-2
x+b经过点G(-2,2)时,2=-2![]() +b,b=2+2
+b,b=2+2![]() ,当一次函数y=
,当一次函数y=![]() x+b经过点P(-2,0)时,0=-2
x+b经过点P(-2,0)时,0=-2![]() +b,b=2
+b,b=2![]() ,观察图象结合图形W1和图形W2是“中心轴对称”的定义可知,当2
,观察图象结合图形W1和图形W2是“中心轴对称”的定义可知,当2![]() ≤b≤2+2
≤b≤2+2![]() 时,线段MN与四边形GHJK是“中心轴对称”的.再根据对称性,求出直线与y轴的负半轴相交时b的范围即可.
时,线段MN与四边形GHJK是“中心轴对称”的.再根据对称性,求出直线与y轴的负半轴相交时b的范围即可.
解:(1)如图1中,

①∵OA=1,OP1=1,OP4=1,
∴P1,P4与点A是“中心轴对称”的,
故答案为P1,P4.
②如图2中,

以O为圆心,OA为半径画弧交射线OB于E,以O为圆心,OC为半径画弧交射线OB于F.
∵在正方形ABCD中,点A(1,0),点C(2,1),
∴点B(1,1),
∵点E在射线OB上,
∴设点E的坐标是(x,y),
则x=y,
即点E坐标是(x,x),
∵点E与正方形ABCD是“中心轴对称”的,
∴当点E与点A对称时,则OE=OA=1,
过点E作EH⊥x轴于点H,则OH2+EH2=OE2,
∴x2+x2=12,
解得x=![]() ,
,
∴点E的横坐标xE=![]() ,
,
同理可求点:F(![]() ,
,![]() ),
),
∵E(![]() ,
,![]() ),F(
),F(![]() ,
,![]() ),
),
∴观察图象可知满足条件的点E的横坐标xE的取值范围:![]() ≤xE≤
≤xE≤![]() .
.
(2)如图3中,设GK交x轴于P.

当一次函数y=![]() x+b经过点G(-2,2)时,2=-2
x+b经过点G(-2,2)时,2=-2![]() +b,b=2+2
+b,b=2+2![]() ,
,
当一次函数y=![]() x+b经过点P(-2,0)时,0=-2
x+b经过点P(-2,0)时,0=-2![]() +b,b=2
+b,b=2![]() ,
,
观察图象结合图形W1和图形W2是“中心轴对称”的定义可知,当2![]() ≤b≤2+2
≤b≤2+2![]() 时,线段MN与四边形GHJK是“中心轴对称”的.
时,线段MN与四边形GHJK是“中心轴对称”的.
根据对称性可知:当-2-2![]() ≤b≤-2
≤b≤-2![]() 时,线段MN与四边形GHJK是“中心轴对称”的.
时,线段MN与四边形GHJK是“中心轴对称”的.
综上所述,满足条件的b的取值范围:2![]() ≤b≤2+2
≤b≤2+2![]() 或-2-2
或-2-2![]() ≤b≤-2
≤b≤-2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,AC是对角线,E是平面内一点,且
 ,过点C作
,过点C作 ,且
,且 。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
。连接AE、AF,M是AF的中点,作射线DM交AE于点N.(1)如图1,若点E,F分别在BC,CD边上。
求证:①
 ;
;②
 ;
;(2)如图2,若点E在四边形ABCD内,点F在直线BC的上方,求
 与
与 的和的度数。
的和的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若
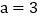 ,
,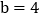 ,则该长方形的面积为__________.
,则该长方形的面积为__________.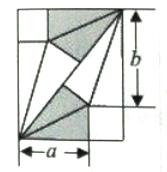
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC,相交于点O,
 cm,
cm, cm,E,F分别是AB,BC的中点,点P是对角线AC上的一个动点,设
cm,E,F分别是AB,BC的中点,点P是对角线AC上的一个动点,设 cm,
cm, cm,
cm, cm
cm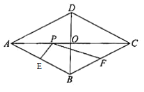
小明根据学习函数的经验,分别对这两种函数随自变量的变化而变化的情况进行了探究,下面是小明探究过程,请补充完整:
(1)画函数
 的图象
的图象①按下表自变量的值进行取点、画图、测量,得到了
 与x的几组对应值:
与x的几组对应值:x/cm
0
0.5
1
1.5
2
2.5
3
3.5
4
 /cm
/cm1.12
0.5
0.71
1.12
1.58
2.06
2.55
3.04
②在所给坐标系中描出补全后的表中的各对应值为坐标的点,画出函数
 的图象;
的图象;
(2)画函数
 的图象
的图象在同一坐标系中,画出函数
 的图象;
的图象;(3)根据画出的函数
 的图象、函数
的图象、函数 的图象,解决问题
的图象,解决问题①函数
 的最小值是________________;
的最小值是________________;②函数
 的图象与函数
的图象与函数 的图象的交点表示的含义是________________;
的图象的交点表示的含义是________________;③若
 ,AP的长约为________________cm
,AP的长约为________________cm -
科目: 来源: 题型:
查看答案和解析>>【题目】某校有A、B两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室阅读.
(1)下列事件中,是必然事件的为( )
A.甲、乙同学都在A阅览室 B.甲、乙、丙同学中至少两人在A阅览室
C.甲、乙同学在同一阅览室 D.甲、乙、丙同学中至少两人在同一阅览室
(2)用画树状图的方法求甲、乙、丙三名学生在同一阅览室阅读的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用长度相等的小棒按一定规律摆成的一组图案
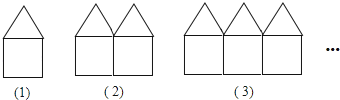
(1)填写下表:
图形序号
①
②
③
……
⑧
每个图案中小棒的数量
6
11
……
(2)请填写出第
 个图案中小棒的数量(用含
个图案中小棒的数量(用含 的代数式表示);
的代数式表示);(3)第30个图案中小棒有多少根?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了开展阳光体育运动,某市教体局做了一个随机调查,调查内容是:每天锻炼是否超过1h及锻炼未超过1h的原因.他们随机调查了600名学生,用所得的数据制成了扇形统计图和频数分布直方图(图1、图2).

根据图示,请回答以下问题:
(1)“没时间”的人数是 ,并补全频数分布直方图;
(2)2016年该市中小学生约40万人,按此调查,可以估计2016年全市中小学生每天锻炼超过1h的约有 万人;
(3)在(2)的条件下,如果计划2018年该市中小学生每天锻炼未超过1h的人数降到7.5万人,求2016年至2018年锻炼未超过1h人数的年平均降低的百分率.
相关试题

