【题目】实验探究:
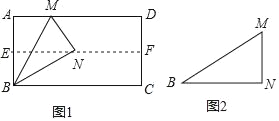
(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.
参考答案:
【答案】(1)猜想:∠MBN=30°,理由见解析;(2)结论:MN=![]() BM.折纸方案及证明见解析.
BM.折纸方案及证明见解析.
【解析】试题分析:(1)猜想:∠MBN=30°.只要证明△ABN是等边三角形即可;
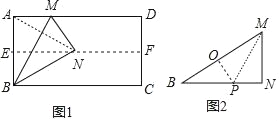
(2)结论:MN=![]() BM.折纸方案:如图,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.由折叠可知△MOP≌△MNP,只要证明△MOP≌△BOP,即可推出MO=BO=
BM.折纸方案:如图,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.由折叠可知△MOP≌△MNP,只要证明△MOP≌△BOP,即可推出MO=BO=![]() BM;
BM;
试题解析:(1)猜想:∠MBN=30°.
理由:如图1中,连接AN,∵直线EF是AB的垂直平分线,
∴NA=NB,
由折叠可知,BN=AB,
∴AB=BN=AN,
∴△ABN是等边三角形,
∴∠ABN=60°,
∴NBM=∠ABM=![]() ∠ABN=30°.
∠ABN=30°.
(2)结论:MN=![]() BM.
BM.
折纸方案:如图2中,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.
理由:由折叠可知△MOP≌△MNP,
∴MN=OM,∠OMP=∠NMP=![]() ∠OMN=30°=∠B,
∠OMN=30°=∠B,
∠MOP=∠MNP=90°,
∴∠BOP=∠MOP=90°,
∵OP=OP,
∴△MOP≌△BOP,
∴MO=BO=![]() BM,
BM,
∴MN=![]() BM.
BM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3﹣4= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并完成填空.
你能比较2 0132 014和2 0142 013的大小吗?
为了解决这个问题,先把问题一般化,比较nn+1和(n+1)n(n≥1,且n为整数)的大小.然后从分析n=1,n=2,n=3…的简单情形入手,从中发现规律,经过归纳、猜想得出结论.
(1)通过计算(可用计算器)比较下列①~⑦组两数的大小:(在横线上填上“>”“=”或“<”)
①12__________21;②23__________32;③34__________43;④45__________54;⑤56__________65;⑥67__________76;⑦78__________87;
(2)归纳第(1)问的结果,可以猜想出nn+1和(n+1)n的大小关系;
(3)根据以上结论,可以得出2 0132 014和2 0142 013的大小关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解.
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE.
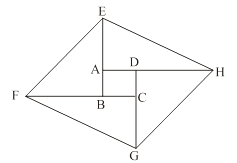
(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长. -
科目: 来源: 题型:
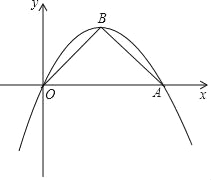
查看答案和解析>>【题目】如图,在平面直角坐标系xOy,已知二次函数y=﹣
 x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.(1)求二次函数的表达式;
(2)若C是BO的中点,点Q在线段AB上,设点B关于直线CQ的对称点为B',当△OCB'为等边三角形时,求BQ的长度;
(3)若点D在线段BO上,OD=2DB,点E、F在△OAB的边上,且满足△DOF与△DEF全等,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用不等式的基本性质求下列不等式的解集,并说出变形的依据.
(1)若x+2 012>2 013,则x__________;(______________________________)
(2)若2x>-
 ,则x__________;(______________________________)
,则x__________;(______________________________)(3)若-2x>-
 ,则x__________;(______________________________)
,则x__________;(______________________________)(4)若-
 >-1,则x__________.(______________________________)
>-1,则x__________.(______________________________) -
科目: 来源: 题型:
查看答案和解析>>【题目】指出下列各式成立的条件:
(1)由mx<n,得x<
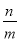 ;
;(2)由a<b,得ma>mb;
(3)由a>-5,得a2≤-5a;
(4)由3x>4y,得3x-m>4y-m.
相关试题

