搜索
【题目】小明、小华用方块2、黑桃4、黑桃5、梅花5四张扑克牌玩游戏，他俩将扑克牌洗匀后，背面朝上放置在桌面上，小明先抽，小华后抽，抽出的牌不放回.
（1）若小明恰好抽到了黑桃4;
①请在方框中绘制这种情况的树状图;
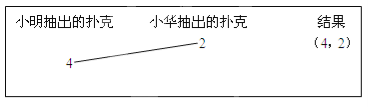
②求小华抽出的牌的牌面数字比4大的概率;
（2）小明、小华约定：只抽一次，若小明抽到牌的牌面数字比小华的大，则小明胜；反之，则小明负。你认为这个游戏是否公平？说明理由.
参考答案：
【答案】（1）①树状图见解析; ②
;（2）不公平，理由见解析.
【解析】
试题分析：（1）因为抽出的牌不放回，所以当小明恰好抽到了黑桃4时，小华只能从剩下的三张牌中抽出；
（2）首先求得小明胜的概率，根据概率可以调整牌，使得规则公平．
试题解析：（1）①树状图绘制如下:
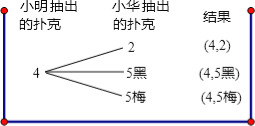
②小华抽出的牌的牌面数字比4大的概率=.
（2）不公平，理由为：
绘制树状图如下
则小明胜的概率是
，小华胜的概率是
.∴不公平.
-
科目： 来源： 题型：
查看答案和解析>>【题目】推理填空：如图，E点为DF上的点，B为AC上的点，
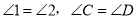，那么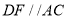
，请完成它成立的理由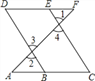
解：
______ 
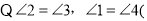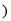
又
______ 
______ 
______ 
______ 
______ 
______ 
______ 
______ 
-
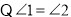
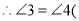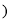
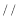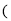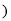
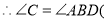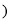
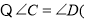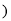
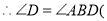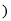
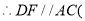科目： 来源： 题型：
查看答案和解析>>【题目】如图是9×7的正方形点阵，其水平方向和竖起直方向的两格点间的长度都为1个单位，以这些点为顶点的三角形称为格点三角形．请通过画图分析、探究回答下列问题：
(1)请在图中画出以AB为边且面积为2的一个网格三角形；
(2)任取该网格中能与A、B构成三角形的一点M，求以A、B、M为顶点的三角形的面积为2的概率；
(3)任取该网格中能与A、B构成三角形的一点M，求以A、B、M为顶点的三角形为直角三角形的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】两人要去某风景区游玩，每天某—时段开往该风景区有三辆汽车(票价相同)，但是他们不知道这些车的舒适程度，也不知道汽车开过来的顺序，两人采用了不同的乘车方案：
甲无论如何总是上开来的第一辆车，而乙则是先观察后上车，当第一辆车开来时，他不上车，而是仔细观察车的舒适状况，如果第二辆乍的状况比第一辆好，他就上第二辆车；如果第二辆不比第—辆好，他就上第三辆车．若把这三辆车的舒适程度分为上、中、下三等.请问：
(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为甲、乙两人采用的方案，哪一种方案使自己乘坐上等车的可能性大?为什么?
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的袋中装有红、黄、白三种颜色球共100个，它们除颜色外都相同，其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是
.（1）求袋中红球的个数；
（2）求从袋中摸出一个球是白球的概率；
（3）取走10个球（其中没有红球）后，求从剩余的球中摸出一个球是红球的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】仔细阅读材料，再尝试解决问题：
完全平方式
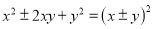以及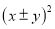
的值为非负数的特点在数学学习中有广泛的应用，比如探求
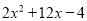的最大（小）值时，我们可以这样处理：解：原式 =
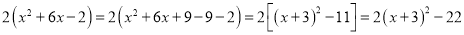.因为无论
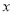取什么数，都有
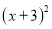的值为非负数，所以
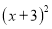的最小值为0；此时
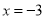时，进而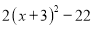
的最小值是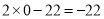
；所以当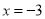
时，原多项式的最小值是
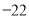.请根据上面的解题思路，探求：
⑴.多项式
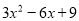的最小值是多少，并写出对应的
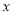的取值；⑵.多项式
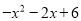的最大值是多少，并写出对应的
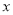的取值. -
科目： 来源： 题型：
查看答案和解析>>【题目】根据下列证明过程填空：
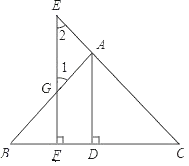
已知：如 图，AD⊥BC于点D，EF⊥BC于点F，交AB于点G，交CA的延长线于点E，∠1=∠2．
求证：AD平分∠BAC，填写证明中的空白．
证明：
∵AD⊥BC，EF⊥BC （已知），
∴EF∥AD （ ），
∴ = （ 两直线平行，内错角相等 ），
=∠CAD （ ）．
∵ （已知），
∴ ，即AD平分∠BAC （ ）．
相关试题
