【题目】(1)如图1,∠AOB和∠COD都是直角
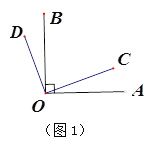
①若∠BOC=60°,则∠BOD= °,∠AOC= °;
②改变∠BOC的大小,则∠BOD与∠AOC相等吗?为什么?
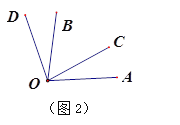
(2)如图2,∠AOB=∠COD=80°,若∠AOD=∠BOC+40°,求∠AOC的度数;
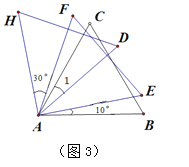
(3)如图3,将三个相同的等边三角形(三个内角都是60°)的一个顶点重合放置,若∠BAE=10°, ∠HAF=30°,则∠1= °.
参考答案:
【答案】(1) ① 30°, 30°, ②相等,同角的余角相等;(2)20°;(3)20°.
【解析】试题分析:(1)根据余角的性质即可得到结论; (2)根据角的和差即可得到结果; (3)根据等边三角形的性质得到∠DAH=∠EAF=∠BAC=60°,根据角的和差即可得到结论.
试题解析:
(1) ①∵∠AOB和∠COD都是直角,∠BOC=60°,
∴∠BOD=30°,∠AOC=30°;
②∠BOD=∠AOC,根据同角的余角相等可得结论;
(2) ∵∠AOB=∠COD=80°,
∴∠AOC=∠BOD=![]() ,
,
∵∠AOD=∠BOC+40°,
∴∠AOC=20°;
(3) ∵∠DAH=∠EAF=∠BAC=60°,
∴∠DAE=∠HAF=30°,
∴∠1=60°-30°-10°=20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名学生军训时连续射靶10次,命中环数分别为 7,8,6,8,5,9,10,7,6,4.则这名学生射击环数的方差是( )
A. 3 B. 2.9 C. 2.8 D. 2.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的“折中点”.如图,点D是折线A﹣C﹣B的“折中点”,请解答以下问题:

(1)当AC>BC时,点D在线段 上; 当AC=BC时,点D与 重合;当AC<BC时,点D在线段 上;
(2)若AC=18cm,BC=10cm,若∠ACB=90°,有一动点P从C点出发,在线段CB上向点B运动,速度为2cm/s, 设运动时间是t(s), 求当t为何值,三角形PCD 的面积为10
 ?
?(3)若E为线段AC中点,EC=8cm,CD=6cm,求CB的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明妈妈经营一家服装专卖店,为了合理利用资金,小明帮妈妈对上个月各种型号的服装销售数量进行了一次统计分析,决定在这个月的进货中多进某种型号服装,此时小明应重点参考( )
A. 众数 B. 平均数 C. 加权平均数 D. 中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运20千克,A型机器人搬运1000千克所用时间与B型机器人搬运800千克所用时间相等,两种机器人每小时分别搬运多少化工原料?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了有效控制酒后驾车,西安市城管的汽车在一条东西方向的公路上巡逻,如果规定向东为正,向西为负,从出发点开始所走的路程为:
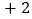 ,
,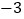 ,
,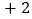 ,
,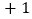 ,
,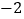 ,
,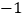 ,
,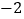 (单位:千米)
(单位:千米)(1)此时,这辆城管的汽车司机如何向队长描述他的位置?
(2)如果队长命令他马上返回出发点,这次巡逻(含返回)共耗油多少升?(已知每千米耗油
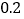 升)
升) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
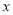 的多项式
的多项式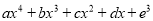 ,其
,其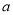 ,
, 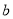 ,
, 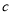 ,
, 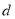 为互不相等的整数,且
为互不相等的整数,且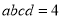 .
.(
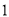 )求
)求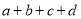 的值.
的值.(
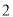 )当
)当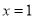 时,这个多项式
时,这个多项式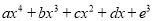 的值为
的值为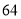 .求
.求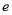 的值.
的值.(
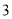 )当
)当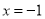 时,求这个多项式
时,求这个多项式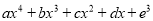 的所有可能的值.
的所有可能的值.
相关试题

