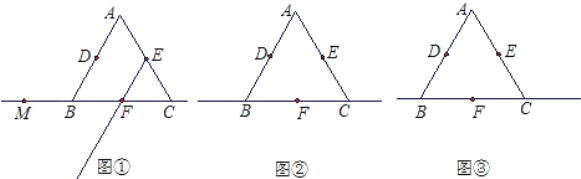
【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?画出图形,不要求证明.
参考答案:
【答案】(1)△DMN是等边三角形;(2)△DMN仍是等边三角形;(3)△DMN不是等边三角形.
【解析】
(1)连接DF,根据等边三角形的性质与三角形中位线平行于第三边并且等于第三边的一半的性质可以证明DF=BD=EF=BF,然后证明BM=FN,∠MBD=∠NFD=120°,从而证明△BDM与△FDN全等,根据全等三角形对应边相等可得MD=DN,对应角相等可得∠MDB=∠NDF,然后证明∠MDN=∠BDF=60°,所以△DMN是等边三角形;
(2)连接DF,根据等边三角形的性质与三角形中位线平行于第三边并且等于第三边的一半的性质可以证明DF=BD=EF=BF,然后证明BM=FN,∠MBD=∠NFD=60°,从而证明△BDM与△FDN全等,根据全等三角形对应边相等可得MD=DN,对应角相等可得∠MDB=∠NDF,然后证明∠MDN=∠BDF=60°,所以△DMN是等边三角形;(3)沿用前两问的思路,显然不能证明△CDM与△FDN全等,所以△DMN不是等边三角形.
(1)如图①,△DMN是等边三角形.

(2)如图②,当M在线段BF上(与点B、F不重合)时,△DMN仍是等边三角形

证明:连接DF,
∵△ABC是等边三角形,∴∠ABC=60°,AB=AC=BC.
∵D、E、F分别是△ABC三边的中点,∴DF=BD=EF=BF
∴∠BDF=∠A=∠DFE=60°,∴∠ABC=∠DFE,
∵FM=EN,∴BM=NF,∴△BDM≌△FDN,
∴∠BDM=∠FDN,MD=ND,
∴∠BDM+∠MDF=∠FDN+∠MDF=∠MDN=60°,
△DMN是等边三角形;
(3)如图③或图④,当点M在射线FC上(与点F不重合)时,(1)中的结论不成立,
即△DMN不是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )

A. =
= 
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.连接CE.求∠E的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请按要求完成下面三道小题.
(1)如图1,AB=AC.这两条线段一定关于某条直线对称吗?如果是,请说明是哪条直线,并在图1中画出这条直线;如果不是,请说明理由.

(2)如图2,已知线段AB和点C.
求作线段CD,使它与AB成轴对称,且A与C是对称点,请画出图形,并简述画图过程.

(3)如图3,任意位置的两条线段AB,CD,AB=CD.你能通过对其中一条线段作有限次的轴对称使它们重合吗?如果能,请画出图形,并描述操作过程;如果不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题,真命题是( )

A.如图,如果OP平分∠AOB,那么,PA=PB
B.三角形的一个外角大于它的一个内角
C.如果两条直线没有公共点,那么这两条直线互相平行
D.有一组邻边相等的矩形是正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为
 的线段的概率为( )
的线段的概率为( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校有一块长方形活动场地,长为
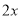 米,宽比长少
米,宽比长少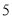 米,实施“阳光体育”行动以后,学校为了扩大学生的活动场地,让学生能更好地进行体育活动,将操场的长和宽都增加
米,实施“阳光体育”行动以后,学校为了扩大学生的活动场地,让学生能更好地进行体育活动,将操场的长和宽都增加 米.
米.(1)求活动场地原来的面积是多少平方米.(用含
 的代数式表示)
的代数式表示)(2)若
 ,求活动场地面积增加后比原来多多少平方米.
,求活动场地面积增加后比原来多多少平方米.
相关试题

