【题目】定义:如图1,抛物线![]() 与
与![]() 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足![]() ,则称点P为抛物线
,则称点P为抛物线![]() 的勾股点。
的勾股点。
(1)直接写出抛物线![]() 的勾股点的坐标;
的勾股点的坐标;
(2)如图2,已知抛物线C:![]() 与
与![]() 轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1,![]() )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件![]() 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标

参考答案:
【答案】(1)(0,1);(2)y=﹣![]() x2+
x2+![]() x;(3)(3,
x;(3)(3,![]() )或(2+
)或(2+![]() ,﹣
,﹣![]() )或(2﹣
)或(2﹣![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)根据抛物线勾股点的定义即可求解;
(2)作PG⊥x轴,由P点坐标求得AG=1、PG=![]() 、 PA=2,由tan∠PAB=
、 PA=2,由tan∠PAB=![]() 知∠PAG=60°,从而求得AB=4,即B(4,0),运用待定系数法即可求解;
知∠PAG=60°,从而求得AB=4,即B(4,0),运用待定系数法即可求解;
(3)由SΔABQ=SΔABP且两三角形同底,可知点Q到x轴的距离为![]() ,据此可求解.
,据此可求解.
试题解析: (1)抛物线y=﹣x2+1的勾股点的坐标为(0,1);
(2)抛物线y=ax2+bx过原点,即点A(0,0),
如图,作PG⊥x轴于点G,
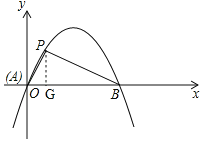
∵点P的坐标为(1,![]() ),
),
∴AG=1、PG=![]() ,PA=
,PA=![]() =2,
=2,
∵tan∠PAB=![]() ,
,
∴∠PAG=60°,
在Rt△PAB中,AB=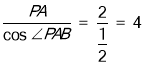 ,
,
∴点B坐标为(4,0),
设y=ax(x﹣4),
将点P(1,![]() )代入得:a=﹣
)代入得:a=﹣![]() ,
,
∴y=﹣![]() x(x﹣4)=﹣
x(x﹣4)=﹣![]() x2+
x2+![]() x;
x;
(3)①当点Q在x轴上方时,由S△ABQ=S△ABP知点Q的纵坐标为![]() ,
,
则有﹣![]() x2+
x2+![]() x =
x =![]() ,
,
解得:x1=3,x2=1(不符合题意,舍去),
∴点Q的坐标为(3,![]() );
);
②当点Q在x轴下方时,由S△ABQ=S△ABP知点Q的纵坐标为﹣![]()
则有﹣![]() x2+
x2+![]() x =﹣
x =﹣![]() ,
,
解得:x1=2+![]() ,x2=2﹣
,x2=2﹣![]() ,
,
∴点Q的坐标为(2+![]() ,﹣
,﹣![]() )或(2﹣
)或(2﹣![]() ,﹣
,﹣![]() );
);
综上,满足条件的点Q有3个:(3,![]() )或(2+
)或(2+![]() ,﹣
,﹣![]() )或(2﹣
)或(2﹣![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设
 ,
, ,
,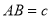 ,请探索
,请探索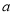 ,
, ,
, 满足的等量关系。
满足的等量关系。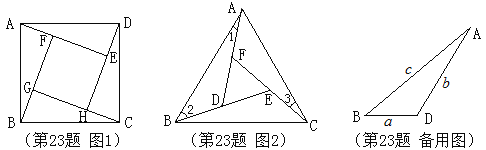
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(+5)-(-3)+(-7)-(+12)
-
科目: 来源: 题型:
查看答案和解析>>【题目】①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线相等.以上四个条件中可以判定四边形是平行四边形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a﹣3b=5ab
B.a2a3=a5
C.(2a)3=6a3
D.a6+a3=a9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
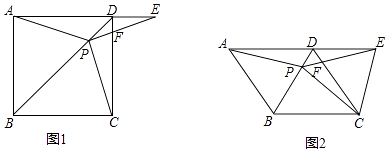
(1)求证:PC=PE;
(2)图1中与∠EAP相等的角是和 , 则可求∠CPE=°;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,请直接写出∠CPE=°.
相关试题

