【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.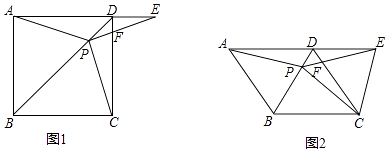
(1)求证:PC=PE;
(2)图1中与∠EAP相等的角是和 , 则可求∠CPE=°;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,请直接写出∠CPE=°.
参考答案:
【答案】
(1)证明:∵四边形ABCD为正方形,
∴BA=BC,∠ABD=∠CBD=45°,
在△ABP和△CBP中
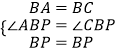 ,
,
∴△ABP≌△CBP,
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)∠E,∠PCD,90
(3)60
【解析】(2)解:∵△ABP≌△CBP,
∴∠PAB=∠PCB,
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAE=∠E,
∴∠PCD=∠E,
而∠DFE=∠PFC,
∴∠CPF=∠EDF=90°,
即图1中与∠EAP相等的角是∠E和∠PCD;
⑶∵四边形ABCD为菱形,
∴BA=BC,∠ABD=∠CBD=60°,∠ADC=∠ABC=120°,
∴∠EDC=60°,
在△ABP和△CBP中
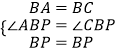 ,
,
∴△ABP≌△CBP,
∴PA=PC,∠PAB=∠PCB,
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAD=∠PED,
∴∠PCD=∠PED,
而∠DFE=∠PFC,
∴∠CPF=∠EDF=60°.
故答案为∠E,∠PCD,90,60.
(1)四边形ABCD为正方形,得到BA=BC,∠ABD=∠CBD=45°,△ABP≌△CBP,得到PA=PC,由PA=PE,得到PC=PE;(2)由△ABP≌△CBP,得到∠PAB=∠PCB,∠PAD=∠PCD,由PA=PE,得到∠PAE=∠E,∠PCD=∠E,而∠DFE=∠PFC,得到∠CPF=∠EDF=90°,即图1中与∠EAP相等的角是∠E和∠PCD;⑶由四边形ABCD为菱形,得到BA=BC,∠ABD=∠CBD=60°,∠ADC=∠ABC=120°,∠EDC=60°,△ABP≌△CBP,得到PA=PC,∠PAB=∠PCB,∠PAD=∠PCD,由PA=PE,得到∠PAD=∠PED,∠PCD=∠PED,而∠DFE=∠PFC,得到∠CPF=∠EDF=60°;故答案为∠E,∠PCD,90,60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,抛物线
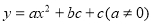 与
与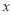 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足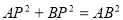 ,则称点P为抛物线
,则称点P为抛物线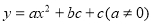 的勾股点。
的勾股点。(1)直接写出抛物线
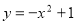 的勾股点的坐标;
的勾股点的坐标;(2)如图2,已知抛物线C:
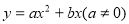 与
与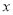 轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1,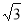 )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;(3)在(2)的条件下,点Q在抛物线C上,求满足条件
 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a﹣3b=5ab
B.a2a3=a5
C.(2a)3=6a3
D.a6+a3=a9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,某班两名同学分别进行了5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的( )
A.平均数
B.频数分布
C.中位数
D.方差 -
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段为边,能组成三角形的是( )
A. 2cm、2cm、4cmB. 2cm、6cm、3cm
C. 8cm、6cm、3cmD. 11cm、4cm、6cm
-
科目: 来源: 题型:
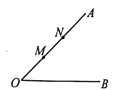
查看答案和解析>>【题目】如图,∠AOB=45°,点M、N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P、M、N构成等腰三角形的点P恰好有三个,则x的值是 .
相关试题

