【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm , 点P从点A出发,沿AB方向以每秒 ![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( ).
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( ).
A.![]()
B.2
C.2 ![]()
D.3
参考答案:
【答案】B
【解析】连接PP′交BC于O ,
∵若四边形QPCP′为菱形,
∴PP′⊥QC ,
∴∠POQ=90°,
∵∠ACB=90°,
∴PO∥AC ,
∴ ![]() ,
,
∵设点Q运动的时间为t秒,
∴AP= ![]() t , QB=t ,
t , QB=t ,
∴QC=6-t ,
∴CO=3- ![]() ,
,
∵AC=CB=6,∠ACB=90°,
∴AB= ![]() =6
=6 ![]() ,
,
∴ 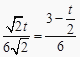 ,
,
解得:t=2,
故选:B.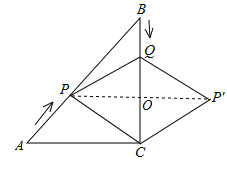
【考点精析】通过灵活运用勾股定理的概念和菱形的性质,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x+2k-2=0有两个不相等的实数根.求k的取值范围.
-
科目: 来源: 题型:
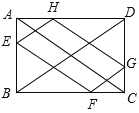
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG , EH∥BD∥FG , 则四边形EFGH的周长是( ).
A.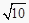
B.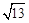
C.2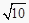
D.2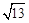
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC , 按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF .
若BD=6,AF=4,CD=3,则BE的长是( ).
A.2
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,E、F分别是边BC , CD上的点,且EF∥BD , AE、AF分别交BD与点G和点H , BD=12,EF=8.求:
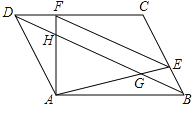
(1) 的值;
的值;
(2)线段GH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组线段中,不构成比例线段的一组是( ).
A.1cm,2cm,3cm,6cm
B.2cm,3cm,4cm,6cm
C.1cm,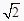 cm,
cm, 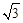 cm,
cm, 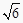 cm
cm
D.1cm,2cm,3cm,4cm -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段d是线段a、b、c的第四比例项,其中a=2cm,b=4cm,c=5cm,则d等于( ).
A.1cm
B.10cm
C.2.5cm
D.1.6cm
相关试题

