搜索
【题目】已知关于x的一元二次方程x2+2x+2k-2=0有两个不相等的实数根．求k的取值范围.
参考答案：
【答案】解答：∵关于x的一元二次方程x2+2x+2k-2=0有两个不相等的实数根，
∴△＞0，
∴△=22-4（2k-2）=4-8k+8=12-8k ，
∴12-8k＞0，
∴k＜ 
【解析】根据一元二次方程x2+2x+2k-2=0有两个不相等的实数根可得△=22-4（2k-2）=4-8k+8=12-8k＞0，求出k的取值范围
【考点精析】利用求根公式对题目进行判断即可得到答案，需要熟知根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算:（1）
（2）
（3）
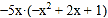（4）（3x+y）(-y+3x)（5）2a(a-2a3)-(-3a2)2； （6）(x-3)(x+2)-(x+1)2
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．
解：设x2－4x=y
原式=（y+2）（y+6）+4 （第一步）
=y2+8y+16 （第二步）
=（y+4）2（第三步）
=（x2－4x+4）2（第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的_______．
A．提取公因式
B．平方差公式
C．两数和的完全平方公式
D．两数差的完全平方公式
（2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果_________ ．
（3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的一元二次方程x2+（2k+1）x+k2+1=0有两个不等实根x1 ， x2 ． 求实数k的取值范围.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AB=2，BC=3，点E、F、G、H分别在矩形ABCD的各边上，EF∥AC∥HG ， EH∥BD∥FG ， 则四边形EFGH的周长是（ ）.
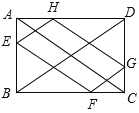
A.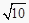
B.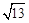
C.2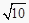
D.2 -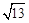
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD平分∠BAC ， 按如下步骤作图：
第一步，分别以点A、D为圆心，以大于
AD的长为半径在AD两侧作弧，交于两点M、N；
第二步，连接MN分别交AB、AC于点E、F；
第三步，连接DE、DF ．
若BD=6，AF=4，CD=3，则BE的长是（ ）.
A.2
B.4
C.6
D.8 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，AC=BC=6cm ， 点P从点A出发，沿AB方向以每秒
cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将△PQC沿BC翻折，点P的对应点为点P′．设点Q运动的时间为t秒，若四边形QPCP′为菱形，则t的值为（ ）.
A.
B.2
C.2
D.3
相关试题
