【题目】为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.
参考答案:
【答案】(1) A型污水处理设备每周每台可以处理污水240 t,B型污水处理设备每周每台可以处理污水200 t(2)购买A型污水处理设备13台,购买B型污水处理设备7台时,所需资金最少,最少是226万元
【解析】(1)根据1台A型污水处理设备+2台B型污水处理设备=每周可以处理污水640吨,2台A型污水处理设备+3台B型污水处理设备=每周可以处理污水1080吨,关系式列出二元一次方程组,从而解答即可;
(2)根据题意可以列出相应的不等式组求出购买A型污水处理设备台数取值范围,从而可以得到购买方案,算出每种方案购买资金即可得解.
解:(1)设A型污水处理设备每周每台可以处理污水x吨,B型污水处理设备每周每台可以处理污水y吨,
由题意得, ![]() ,解得,
,解得, ![]() ,
,
即A型污水处理设备每周每台可以处理污水240吨,B型污水处理设备每周每台可以处理污水200吨;
(2)设购买A型污水处理设备x台,则购买B型污水处理设备(20﹣x)台,
则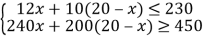 ,解得,12.5≤x≤15,
,解得,12.5≤x≤15,
第一种方案:当x=13时,20﹣x=7,花费的费用为:13×12+7×10=226万元;
第二种方案:当x=14时,20﹣x=6,花费的费用为:14×12+6×10=228万元;
第三种方案;当x=15时,20﹣x=5,花费的费用为:15×12+5×10=230万元;
即购买A型污水处理设备13台,则购买B型污水处理设备7台时,所需购买资金最少,最少是226万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
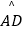 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H. 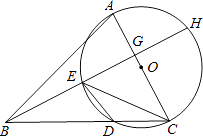
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分) 如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点是C(0,a)(a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.
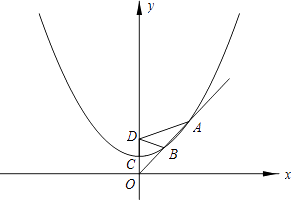
(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线上任意一点,过P作PH丄x轴.垂足是H,求证:PD=PH;
(3)设过原点O的直线l与抛物线在笫一象限相交于A、B两点,若DA=2DB.且S△ABD=4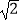 .求a的值.
.求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?
(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形具有四条对称轴的是( )
A.等边三角形B.平行四边形C.矩形D.正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为( )

A.1
B.
C.2
D.2
相关试题

