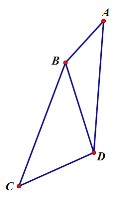
【题目】如图,BD为四边形ABCD的对角线,BC=AD,∠A=∠CBD,∠ABD=120°,AB=3,CD=![]() ,则BC的长为_____________.
,则BC的长为_____________.
参考答案:
【答案】7
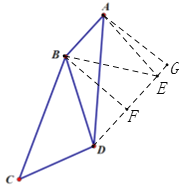
【解析】如图,过点D作DE//BA,并且使DE=BD,连接BE,AE,过点B作BF⊥DE于点F,过点A作AG⊥DE于点G,则四边形ABFG是矩形,从而有FG=AB=3,AG=BF,通过证明△ADE≌△CBD,可得AE=CD=![]() ,根据已知易得△BDE是等边三角形,根据等边三角形的性质可得DF=
,根据已知易得△BDE是等边三角形,根据等边三角形的性质可得DF=![]() BD,BF=
BD,BF=![]() BD,在Rt△AEG中,利用勾股定理可求得BD=5,从而得AG=
BD,在Rt△AEG中,利用勾股定理可求得BD=5,从而得AG=![]() ,DG=
,DG=![]() ,在Rt△ADG中,根据勾股定理求得AD长即可得答案.
,在Rt△ADG中,根据勾股定理求得AD长即可得答案.
如图,过点D作DE//BA,并且使DE=BD,连接BE,AE,过点B作BF⊥DE于点F,过点A作AG⊥DE于点G,则四边形ABFG是矩形,
∴FG=AB=3,AG=BF,
∵AB//DE,∴∠ADE=∠BAD,
∵∠BAD=∠CBD,
∴∠ADE=∠CBD,
又∵DE=BD,AD=BC,
∴△ADE≌△CBD,
∴AE=CD=![]() ,
,
∵∠ABD=120°,DE//AB,
∴∠BDE=60°,
∴△BDE是等边三角形,
∴DF=![]() BD,BF=
BD,BF=![]() BD,
BD,
在Rt△AEG中, AE2=AG2+EG2,EG=DF+FG-DE=![]() BD+3-BD=3-
BD+3-BD=3-![]() BD,
BD,
∴![]() ,
,
∴BD=5或BD=-2(舍去),
∴AG=![]() ,DG=DF+FG=
,DG=DF+FG=![]() +3=
+3=![]() ,
,
在Rt△ADG中,AD2=AG2+DG2=(![]() )2+(
)2+(![]() )2=49,
)2=49,
∴AD=7,
∴BC=7,
故答案为:7.
-
科目: 来源: 题型:
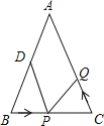
查看答案和解析>>【题目】如图,已知△ABC中,∠B=∠C,BC=8cm,BD=6cm如果点P在线段BC上以1cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,设点Q的速度为xcm/s,则当△BPD与△CQP全等时,x=______.
-
科目: 来源: 题型:
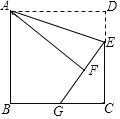
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且DE=2.将△ADE沿AE对折得到△AFE,延长EF交边BC于点G,则BG=___________.
-
科目: 来源: 题型:
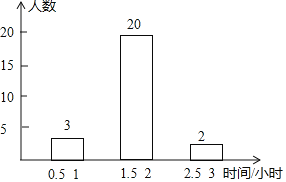
查看答案和解析>>【题目】某校七年级开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现,学校随机抽查了部分学生在这次活动中做家务的时间,并绘制了如下的频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
等级
做家务时间(小时)
频数
百分比
A
0.5≤x<1
3
6%
B
1<x<1.5
a
30%
C
1.5≤x<2
20
40%
D
2≤x<2.5
b
m
E
2.5≤x<3
2
4%
(1)这次活动中抽查的学生有______人,表中a=______,b=______,m=______,并补全频数分布直方图;
(2)若该校七年级有700名学生,请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有多少人?
-
科目: 来源: 题型:
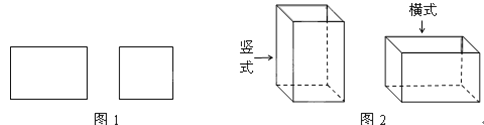
查看答案和解析>>【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图2所示的竖式与横式两种无盖的长方形纸箱(加工时接缝材料不计).
若该厂购进正方形纸板1000张,长方形纸板2000张,问竖式纸盒、横式纸盆各加工多少个,恰好能将购进的纸板全部用完?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产的
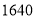 件新产品,需要精加工后才能投放市场.现把精加工新产品的任务分给甲、乙两人,甲加工新产品的数量要比乙多
件新产品,需要精加工后才能投放市场.现把精加工新产品的任务分给甲、乙两人,甲加工新产品的数量要比乙多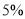 .
.(1)求甲、乙两人各需加工多少件新产品;
(2)已知乙比甲平均每天少加工
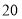 件新产品,用时比甲多用
件新产品,用时比甲多用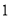 天时间.求甲平均每天加工多少件新产品.
天时间.求甲平均每天加工多少件新产品. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
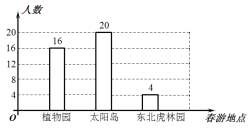
(1)求a的值.
(2)求a名学生中选择去植物园春游的人数占所抽取人数的百分比是多少?
(3)如果该校八年级有440名学生,请你估计选择去太阳岛春游的学生有多少名?
相关试题

