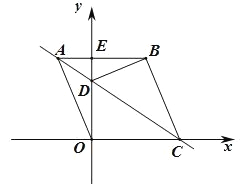
【题目】如图,四边形 ABCO 是菱形,以点 O 为坐标原点,OC 所在直线为![]() 轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与
轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与![]() 轴的交点分别是点 D 与点 E,连接 BD.
轴的交点分别是点 D 与点 E,连接 BD.
(1)求菱形 ABCO 的边长;
(2)求 BD 所在直线的解析式;
(3)直线 AC 上是否存在一点 P 使得![]() 与
与![]() 的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)菱形 ABCO 的边长为 13;(2) BD 所在直线为![]() ;(3)存在点 P 使得△PBD 与△EBD 的面积相等, 点 P 的坐标为
;(3)存在点 P 使得△PBD 与△EBD 的面积相等, 点 P 的坐标为![]() 或
或![]() .
.
【解析】
(1)在Rt△AOE中利用勾股定理即可求得菱形的边长;
(2)根据(1)即可求的OC的长,则C的坐标即可求得,利用待定系数法即可求得直线AC的解析式,求出点D的坐标,再利用待定系数法求BD的解析式即可;
(3)设点P(a,![]() ),根据S△PBD =
),根据S△PBD =![]() =S△EBD列式计算即可.
=S△EBD列式计算即可.
(1)∵四边形 ABCO 为菱形,
∴AB∥CO,
∴∠AEO=∠EOC=90°,
∴在 Rt△EHD 中,
![]() ,
,
∴菱形 ABCO 的边长为 13;
(2)∵四边形 ABCO 为菱形
∴OC=OA=AB=13,
∴BE=AB-AE=13-5=8,
∴点 B 坐标为(8,12),点 C 的坐标为(13,0), 设 AC 所在直线为 y=kx+b,
根据题意得![]() ,
,
解得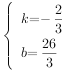 ,
,
![]() ,
,
∴AC 所在直线为![]() ,
,
∴当 x=0 时,
∴点 D 的坐标为![]() ,
,
同上理可得 BD 所在直线为![]() ;
;
(3)存在点 P 使得△PBD 与△EBD 的面积相等, 点 P 的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
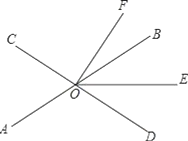
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电实施“阶梯电价”收费,具体收费标准见下表:
一户居民一个月用电量的范围 电费价格(单位:元/千瓦时)
不超过150千瓦时的部分 a
超过150千瓦时,但不超过300千瓦时的部分 b
超过300千瓦时的部分 a+0.3
2015年5月份,该市居民甲用电100千瓦时,交费60元;居民乙用电200千瓦时,交费122.5元.
(1)求上表中a、b的值.
(2)实施“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月交费277.5元?
(3)实施“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月的平均电价等于0.62元/千瓦时?
-
科目: 来源: 题型:
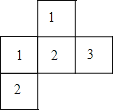
查看答案和解析>>【题目】如图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,请画出这个几何体的主视图和左视图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l上有一点O,点A,B同时从O出发,在直线l上分别向左,向右作匀速运动,且A,B的速度之比是1:2,设运动时间为ts,
(1)当t=2s时,AB=24cm,此时,
①在直线l上画出A,B两点运动2s时的位置,并回答点A运动的速度是 cm/s,点B的运动速度是 cm/s;
②若点P为直线l上一点,且PA=OP+PB,求
 的值;
的值;(2)在(1)的条件下,若A,B同时按原速度向左运动,再经过几秒,OA=3OB?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子中是一元一次方程的是( )
A.
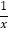 ﹣2=5 B. 2x﹣3 C. x=y D. 3x=0
﹣2=5 B. 2x﹣3 C. x=y D. 3x=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】有一些相同的房间需要粉刷墙面,一天4名一级技工去粉刷10个房间,结果其中有
 墙面未来得及粉刷;同样时间内7名二级技工粉刷了15个房间之外,还多粉刷了另外的
墙面未来得及粉刷;同样时间内7名二级技工粉刷了15个房间之外,还多粉刷了另外的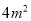 墙面.每名一级技工比二级技工一天多粉刷
墙面.每名一级技工比二级技工一天多粉刷 墙面.设每个房间需要粉刷的墙面面积为
墙面.设每个房间需要粉刷的墙面面积为 平方米,一级技工每天粉刷y平方米,下列方程正确有( )个
平方米,一级技工每天粉刷y平方米,下列方程正确有( )个(1)
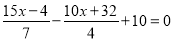 (2)
(2)
(3)
 (4)
(4)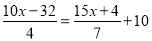
A. 4 B. 3 C. 2 D. 1
相关试题

