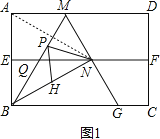
【题目】如图,四边形ABCD是矩形纸片,![]() 对折矩形纸片ABCD,使AD与BC重合折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点
对折矩形纸片ABCD,使AD与BC重合折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点![]() 有如下结论:
有如下结论:![]() ;
;![]() 是等边三角形;
是等边三角形;![]() ;
;![]() 为线段BM上一动点,H是BN的中点,则
为线段BM上一动点,H是BN的中点,则![]() 的最小值是
的最小值是![]() 其中正确结论的个数是
其中正确结论的个数是![]()
![]()

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】B
【解析】
![]() 首先根据EF垂直平分AB,可得
首先根据EF垂直平分AB,可得![]() ;然后根据折叠的性质,可得
;然后根据折叠的性质,可得![]() ,据此判断出
,据此判断出![]() 为等边三角形,即可判断出
为等边三角形,即可判断出![]() 求出
求出![]() ;然后在
;然后在![]() 中,根据
中,根据![]() ,求出AM的大小即可.
,求出AM的大小即可.
![]() 根据对折得
根据对折得![]() ,再由平行线的性质和三角形的内角和定理得:
,再由平行线的性质和三角形的内角和定理得:![]() ,即可推得
,即可推得![]() 是等边三角形.
是等边三角形.
![]() 根据平行线等分线段定理得:
根据平行线等分线段定理得:![]() ,
,![]() ,得QN是
,得QN是![]() 的中位线,可得QN的长;
的中位线,可得QN的长;
![]() 首先根据
首先根据![]() 是等边三角形,点N是MG的中点,判断出
是等边三角形,点N是MG的中点,判断出![]() ,即可求出BN的大小;然后根据E点和H点关于BM称可得
,即可求出BN的大小;然后根据E点和H点关于BM称可得![]() ,因此P与Q重合时,
,因此P与Q重合时,![]() ,据此求出
,据此求出![]() 的最小值是多少即可.
的最小值是多少即可.
![]() 如图1,连接AN,交BM于P,
如图1,连接AN,交BM于P,
![]() 垂直平分AB,
垂直平分AB,
![]() ,
,
根据折叠的性质,可得![]() ,
,
![]() .
.
![]() 为等边三角形.
为等边三角形.
![]() ,
,
![]() ,
,
![]() ,
,
故![]() 不正确;
不正确;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
故![]() 正确;
正确;
![]() 由
由![]() 知:
知:![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
故![]() 不正确.
不正确.
![]() 是等边三角形,点N是MG的中点,
是等边三角形,点N是MG的中点,
![]() ,
,
![]() ,
,
根据条件易知E点和H点关于BM对称,
![]() ,
,
![]() 与Q重合时,
与Q重合时,![]() 的值最小,此时
的值最小,此时![]() ,如图2,
,如图2,

![]() ,
,
![]() 的最小值是
的最小值是![]() ,
,
故![]() 正确.
正确.
本题结论正确的有:![]() ,2个,
,2个,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )

A. 6 B. 8 C. 12 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】2011年11月28日,为扩大内需,国务院决定在全国实施“家电下乡“政策.第一批列入家电下乡的产品为彩电、冰箱、洗衣机和手机四种产品.某县一家家电商场,今年一季度对以上四种产品的销售情况进行了统计,绘制了如下的统计图,根据图中信息求:

(1)彩电占四种家电下乡产品的百分比;
(2)该商场一季度冰箱销售的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至G,使CG=BF,连接CE、DE、DG.

(1)如图1,求证:四边形CEDG是平行四边形;
(2)如图2,连接EG交AC于点H,若EG⊥AB,请直接写出图2中所有长度等于 GH的线段.
GH的线段. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若∠DAC=2∠ABC,AC=BC,四边形ABCD是平行四边形,则∠ABC=____.45°;
(2)如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4.求BD的长;
(3)如图3,若∠ABC=30°,∠ACD=45°,AC=2,B、D之间距离是否有最大值?如有求出最大值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为
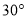 ,底部B点的俯角为
,底部B点的俯角为 ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为 (如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠BCA=90°,BC=AC,直角顶点C在y轴上,锐角顶点A在x轴上.
(1)如图①,若点C的坐标是(0,-1),点A的坐标是(-3,0),求B点的坐标;
(2)如图②,若x轴恰好平分∠BAC,BC与x轴交于点D,过点B作BE⊥x轴于E,问AD与BE有怎样的数量关系,并说明理由;
(3)如图③,直角边AC在两坐标轴上滑动,使点B在第四象限内,过B点作BF⊥x轴于F,在滑动的过程中,猜想OC、BF、OA之间的关系,并证明你的结论.
相关试题

