【题目】如图,△OAB是边长为2的等边三角形,过点A的直线![]() 与z轴交于点E.
与z轴交于点E.
(1)求点E的坐标;
(2)求证OA⊥AE.

参考答案:
【答案】(1)点E(4,0)。(2)证明见解析
【解析】试题分析:(1)过点A作AD⊥EO于点D,根据等腰三角形的性质可得OD=DB=1,再由勾股定理求得AD=![]() ,即可得点A的坐标为(1,
,即可得点A的坐标为(1, ![]() ),用待定系数法求得直线AE的解析式,再求点E的坐标即可;(2)利用E点坐标得出EO的长,进而求出AE的长,再利用勾股定理逆定理得出答案.
),用待定系数法求得直线AE的解析式,再求点E的坐标即可;(2)利用E点坐标得出EO的长,进而求出AE的长,再利用勾股定理逆定理得出答案.
试题解析:
(1)过点A作AD⊥EO于点D,
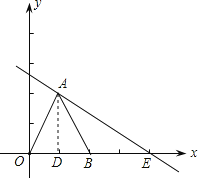
∵△OAB是边长为2的等边三角形,
∴OD=DB=1,AB=AO=OB=2,
∴AD=![]() ,
,
∴A(1,![]() ),
),
将A点代入直线y=-![]() 得:
得:
![]() ,
,
解得:m=![]() ,
,
∴y=-![]() ,
,
则y=0时,x=4,
即E(4,0);
(2) 证明:∵AD=![]() ,DE=EO-DO=3,
,DE=EO-DO=3,
∴AE=![]() ,
,
∵AO2+AE2=16,EO2=16,
∴AO2+AE2=EO2,
∴OA⊥AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学课上,李老师对大家说:“你任意想一个非零数,然后按下列步骤操作,我会直接说出你运算的最后结果.”

(1)若小明同学心里想的是数9,请帮他计算出最后结果: [(9+1)2﹣(9﹣1)2]×25÷9
(2)老师说:“同学们,无论你们心里想的是什么非零数,按照以上步骤进行操作,得到的最后结果都相等.”小明同学想验证这个结论,于是,设心里想的数是a(a≠0),请你帮小明完成这个验证过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L1过A(0,2),B(2,0)两点,直线L2:y=mx+b过点C(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】地表以下岩层的温度t (℃),随着所处的深度 h (km)的变化而变化,t与h 在一定范围内近似成一次函数关系.
(1)根据下表,求 t(℃)与h (km)之间的函数关系式.

(2)求当岩层温度达到 1770 ℃时,岩层所处的深度为多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2-7+5-3;
(2)-
 -
- +
+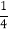 -
- ;
;(3)(-40)-(+27)+19-24-(-32);
(4)0.5-
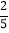 +
+ -
- -
-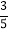 ;
;(5)|-3.5|-
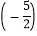 +
+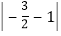
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形ABCD中AE平分∠BAD交BC于E, ∠CAE=15°,则下面的结论:①△ODC是等边三角形; ②BC=2AB; ③∠AOE=135°; ④
 ,其中正确结论有( )
,其中正确结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图示的对话解答下列问题.

求:(1)a,b的值;
(2)8﹣a+b﹣c的值.
相关试题

