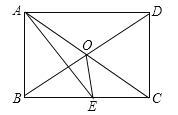
【题目】如图所示,矩形ABCD中AE平分∠BAD交BC于E, ∠CAE=15°,则下面的结论:①△ODC是等边三角形; ②BC=2AB; ③∠AOE=135°; ④![]() ,其中正确结论有( )
,其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】解:∵四边形ABCD是矩形,∴∠BAD=90°,OA=OC,OD=OB,AC=BD,∴OA=OD=OC=OB.∵AE平分∠BAD,∴∠DAE=45°.∵∠CAE=15°,∴∠DAC=30°.∵OA=OD,∴∠ODA=∠DAC=30°,∴∠DOC=60°.∵OD=OC,∴△ODC是等边三角形,∴①正确;
∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°,∴∠DAC=∠ACB=30°,∴AC=2AB.∵AC>BC,∴2AB>BC,∴②错误;
∵AD∥BC,∴∠DBC=∠ADB=30°.∵AE平分∠DAB,∠DAB=90°,∴∠DAE=∠BAE=45°.∵AD∥BC,∴∠DAE=∠AEB,∴∠AEB=∠BAE,∴AB=BE.∵四边形ABCD是矩形,∴∠DOC=60°,DC=AB.∵△DOC是等边三角形,∴DC=OD,∴BE=BO,∴∠BOE=∠BEO=![]() (180°﹣∠OBE)=75°.∵∠AOB=∠DOC=60°,∴∠AOE=60°+75°=135°,∴③正确;
(180°﹣∠OBE)=75°.∵∠AOB=∠DOC=60°,∴∠AOE=60°+75°=135°,∴③正确;
∵OA=OC,∴根据等底等高的三角形面积相等得出S△AOE=SCOE,∴④正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】地表以下岩层的温度t (℃),随着所处的深度 h (km)的变化而变化,t与h 在一定范围内近似成一次函数关系.
(1)根据下表,求 t(℃)与h (km)之间的函数关系式.

(2)求当岩层温度达到 1770 ℃时,岩层所处的深度为多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAB是边长为2的等边三角形,过点A的直线
 与z轴交于点E.
与z轴交于点E.(1)求点E的坐标;
(2)求证OA⊥AE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2-7+5-3;
(2)-
 -
- +
+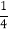 -
- ;
;(3)(-40)-(+27)+19-24-(-32);
(4)0.5-
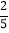 +
+ -
- -
-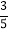 ;
;(5)|-3.5|-
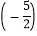 +
+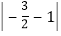
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图示的对话解答下列问题.

求:(1)a,b的值;
(2)8﹣a+b﹣c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的,如果规定向东为正,行车里程(单位:km)如下:
+11, -2, +3, +9, -11, +5, -15, -8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为5元,成本为2.7元/km,则这天下午他盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出
 =83分,
=83分,  =82分,绘制成如下尚不完整的统计图表. 甲、乙两人模拟成绩统计表
=82分,绘制成如下尚不完整的统计图表. 甲、乙两人模拟成绩统计表①
②
③
④
⑤
甲成绩/分
79
86
82
a
83
乙成绩/分
88
79
90
81
72
根据以上信息,回答下列问题:
(1)a=
(2)请完成图中表示甲成绩变化情况的折线.
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.
相关试题

