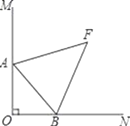
【题目】如图,∠MON=90°,OB=2,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两角平分线所在的直线交于点F,求点A在运动过程中线段BF的最小值为 ______
参考答案:
【答案】![]()
【解析】
作FC⊥OB于C,FD⊥OA于D,FE⊥AB于E,由角平分线的性质得出FD=FC,证出点F在∠MON的平分线上,∠BOF=45°,在点A在运动过程中,当OF⊥BF时,BF最小,△OBF为等腰直角三角形,即可得出BF=![]() OB=
OB=![]() .
.
作FC⊥OB于C,FD⊥OA于D,FE⊥AB于E,如图所示:
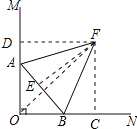
∵∠MAB与∠ABN的角平分线AF与BF交于点F,
∴FD=FE,FE=FC,
∴FD=FC,
∴点F在∠MON的平分线上,∠BOF=45°,
在点A在运动过程中,当OF⊥BF时,F为垂足,BF最小,
此时,△OBF为等腰直角三角形,BF=![]() OB=
OB=![]() ;
;
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

-
科目: 来源: 题型:
查看答案和解析>>【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,
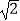 ≈1.414,
≈1.414, 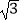 ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 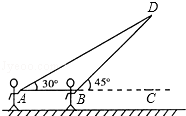
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,3))、B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为
A. (2,0) B. (2.5,0) C. (4,0), D. (4.5,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy,直线y=x﹣1与y轴交于点A,与双曲线y=
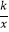 交于点B(m,2)
交于点B(m,2) 
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若△ABC的面积为6,求直线CD的表达式. -
科目: 来源: 题型:
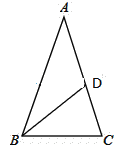
查看答案和解析>>【题目】如图,△ABC中,∠A=36°,∠C=72°,∠DBC=36°.
(1)求∠ABD的度数。
(2)求证:BC=AD.
相关试题

