【题目】”4.20芦山地震”发生后,各地积极展开抗震救援工作,一支救援车队经过如图1所示的一座拱桥,拱桥的轮廓是抛物线型,拱高6m,跨度20m,相邻两支柱间的距离均为5m,将抛物线放在所给的直角坐标系中(如图2所示),拱桥的拱顶在y轴上.
(1)求拱桥所在抛物线的解析式;
(2)求支柱MN的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2米的隔离带),其中的一条行车道能否并排行驶宽2m、高2.4m的三辆汽车(隔离带与内侧汽车的间隔、汽车间的间隔、外侧汽车与拱桥的间隔均为0.5m)?请说说你的理由.
参考答案:
【答案】解:(1)根据题目条件,A、B、C的坐标分别是(﹣10,0)、(10,0)、(0,6).
将B、C的坐标代入y=ax2+c,得![]()
解得a=﹣![]() ,c=6.
,c=6.
所以抛物线的表达式是y=﹣![]() x2+6;
x2+6;
(2)可设N(5,yN),于是yN=﹣![]() ×52+6=4.5.
×52+6=4.5.
从而支柱MN的长度是10﹣4.5=5.5米;
(3)设DE是隔离带的宽,EG是三辆车最内侧与最外侧的宽度和,则G点坐标是(9,0),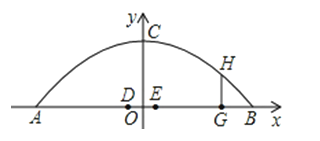
过G点作GH垂直AB交抛物线于H,则yH=﹣![]() ×92+6=1.14<2.4,
×92+6=1.14<2.4,
根据抛物线的特点,可知一条行车道不能并排行驶这样的三辆汽车.
【解析】(1)根据题目可知A.B,C的坐标,设出抛物线的解析式代入可求解;
(2)设N点的坐标为(5,yN)可求出支柱MN的长度;
(3)设DE是隔离带的宽,EG是三辆车的宽度和,作GH垂直AB交抛物线于H,求出GH则可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点C的坐标为(﹣1,1),将Rt△ABC按一定的规律变换:第一次,将Rt△ABC沿AC边翻折,得Rt△AB1C;第二次,将Rt△AB1C绕点B1逆时针旋转90°,得Rt△A1B1C1;第三次,将Rt△A1B1C1沿A1C1边翻折,得Rt△A1B2C1;第四次,将Rt△A1B2C1绕点B2逆时针90°,得Rt△A2B2C2…如此依次下去
(1)试在图中画出Rt△A1B1C1和Rt△A2B2C2 , 并写出A1的坐标 ;
(2)请直接写出在第11次变换后所得的点B的对应的点的坐标是 .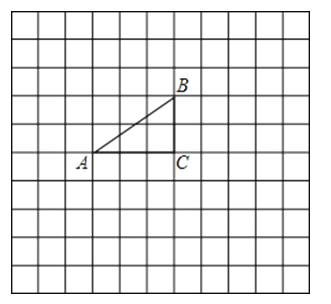
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,O是AB上一点,以OA为半径的⊙O切BC于点D,交AC于点E,且AD=BD.
(1)求证:DE∥AB;
(2)如图2,连接OC,求cos∠ACO的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察某月日历,回答下列问题:
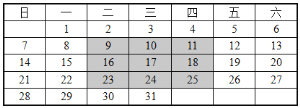
 观察图中的阴影部分的
观察图中的阴影部分的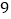 个数,你知道他们之间有什么关系吗?写出你认为正确的一个结论;
个数,你知道他们之间有什么关系吗?写出你认为正确的一个结论;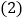 小强一家外出游玩了
小强一家外出游玩了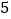 天,这
天,这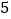 天的日期之和是
天的日期之和是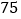 ,小强一家几号外出的?
,小强一家几号外出的?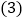 像上面第
像上面第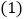 题那样现在要用一个方框去框该月历上的九个数,这九个数的和可能是
题那样现在要用一个方框去框该月历上的九个数,这九个数的和可能是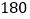 吗?如果不能,请说明理由;如果能,请求出框出的这九个数.
吗?如果不能,请说明理由;如果能,请求出框出的这九个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,抛物线y=x2的顶点在直线AO上运动,与直线x=2交于点P,设平移后的抛物线顶点M的横坐标为m.
(1)如图1,若m=﹣1,求点P的坐标;
(2)在抛物线平移的过程中,当△PMA是等腰三角形时,求m的值;
(3)如图2,当线段BP最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由.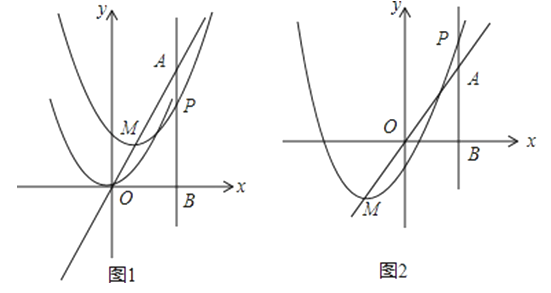
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为﹣7,﹣1,3.乙袋中的三张卡片所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况.
(2)求点A落在第三象限的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列方程,属于一元一次方程的有( )
①x﹣2=
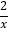 ;②0.5x=1;③
;②0.5x=1;③ =8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.
=8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.A. 5个 B. 4个 C. 3个 D. 2个
相关试题

