【题目】如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,抛物线y=x2的顶点在直线AO上运动,与直线x=2交于点P,设平移后的抛物线顶点M的横坐标为m.
(1)如图1,若m=﹣1,求点P的坐标;
(2)在抛物线平移的过程中,当△PMA是等腰三角形时,求m的值;
(3)如图2,当线段BP最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由.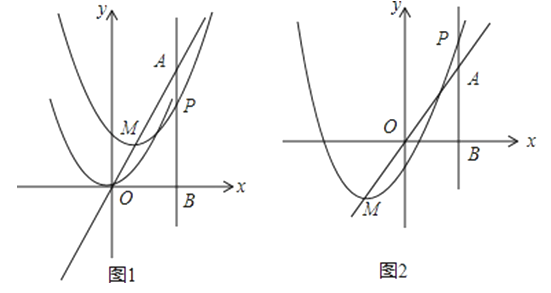
参考答案:
【答案】解:(1)设OA所在直线的函数解析式为y=kx,
∵A(2,4),
∴2k=4,
∴k=2,
∴OA所在直线的函数解析式为y=2x.
由题意,把x=﹣1,代入得,y=﹣2,
∴抛物线的顶点M(﹣1,﹣2),
∴抛物线解析式为:y=(x+1)2﹣2=x2+2x﹣1,
当x=2时,y=7,
∴点P(2,7);
(2)如图1,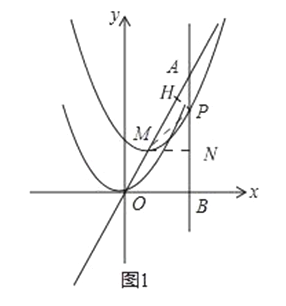
在抛物线平移的过程中,设顶点坐标(m,2m)当△PMA是等腰三角形时,
∴有PA=PM,
由点A(2,4),
可求:tan∠A=![]() ,cos∠A=
,cos∠A=![]() ,
,
过点M作MN垂直于直线x=2,过点P作PH⊥AM,连接MP,
抛物线解析式为:y=(x﹣m)2+2m,
当x=2时,y=m2﹣2m+4,
此时,MN=2﹣m,AN=4﹣2m,
AP=4﹣(m2﹣2m+4)=﹣m2+2m,
∴AH=AP×![]() =
=![]() ,
,
AM=2AH=![]() ,
,
∴![]() =
=![]() ,
,
代入解得:m=![]() ,或m=2(舍去)
,或m=2(舍去)
∴m=![]() ;
;
(3)如图2,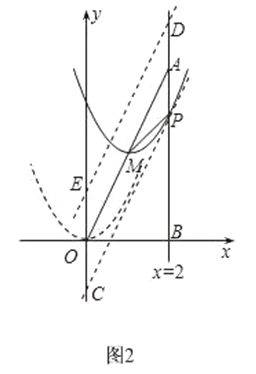
∵顶点M的横坐标为m,且在直线OA上移动,
∴y=2m.
∴顶点M的坐标为(m,2m).
∴抛物线函数解析式为y=(x﹣m)2+2m.
∴当x=2时,y=(2﹣m)2+2m=m2﹣2m+4.
∴点P的坐标是(2,m2﹣2m+4).
∵PB=m2﹣2m+4=(m﹣1)2+3,
∴当m=1时,PB最短.
当线段PB最短时,此时抛物线的解析式为y=(x﹣1)2+2
即y=x2﹣2x+3.
假设在抛物线上存在点Q,使S△QMA=S△PMA .
设点Q的坐标为(x,x2﹣2x+3).
①点Q落在直线OA的下方时,过P作直线PC∥AO,交y轴于点C,
∵PB=3,AB=4,
∴AP=1,
∴OC=1,
∴C点的坐标是(0,﹣1),
∵点P的坐标是(2,3),
∴直线PC的函数解析式为y=2x﹣1,
∵S△QMA=S△PMA ,
∴点Q落在直线y=2x﹣1上,
∴x2﹣2x+3=2x﹣1,
解得x1=2,x2=2,
即点Q(2,3),
∴点Q与点P重合,
∴此时抛物线上存在点Q(2,3),使△QMA与△APM的面积相等,
②当点Q落在直线OA的上方时,
作点P关于点A的对称称点D,过D作直线DE∥AO,交y轴于点E,
∵AP=1,
∴EO=DA=1,
∴E、D的坐标分别是(0,1),(2,5),
∴直线DE函数解析式为y=2x+1,
∵S△QMA=S△PMA ,
∴点Q落在直线y=2x+1上,
∴x2﹣2x+3=2x+1,
解得:x=2+![]() ,或x=2-
,或x=2-![]() ,
,
代入y=2x+1,得:y=5+2![]() 或y=5-2
或y=5-2![]() ,
,
∴△QMA的面积与△PMA的面积相等时,点Q的坐标为:(2+![]() ,5+2
,5+2![]() ),(2-
),(2-![]() ,5-2
,5-2![]() ).
).
【解析】(1)先求出直线OA的解析式,代入m=﹣1,求出抛物线的顶点坐标,即可求出抛物线解析式;
(2)过点M作MN垂直于直线x=2,过点P作PH⊥AM,连接MP,设出抛物线顶点坐标,表示PA,AM,MN,的长度,结合∠A的三角函数列出方程求解即可;
(3)先求出BP最短时的抛物线解析式,设出点Q坐标,根据题意构造平行线,分Q在直线OA的上方和下方两种情况分别列式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,O是AB上一点,以OA为半径的⊙O切BC于点D,交AC于点E,且AD=BD.
(1)求证:DE∥AB;
(2)如图2,连接OC,求cos∠ACO的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察某月日历,回答下列问题:
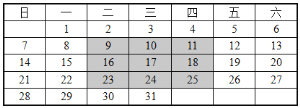
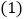 观察图中的阴影部分的
观察图中的阴影部分的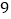 个数,你知道他们之间有什么关系吗?写出你认为正确的一个结论;
个数,你知道他们之间有什么关系吗?写出你认为正确的一个结论;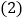 小强一家外出游玩了
小强一家外出游玩了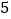 天,这
天,这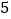 天的日期之和是
天的日期之和是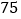 ,小强一家几号外出的?
,小强一家几号外出的?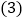 像上面第
像上面第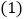 题那样现在要用一个方框去框该月历上的九个数,这九个数的和可能是
题那样现在要用一个方框去框该月历上的九个数,这九个数的和可能是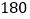 吗?如果不能,请说明理由;如果能,请求出框出的这九个数.
吗?如果不能,请说明理由;如果能,请求出框出的这九个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】”4.20芦山地震”发生后,各地积极展开抗震救援工作,一支救援车队经过如图1所示的一座拱桥,拱桥的轮廓是抛物线型,拱高6m,跨度20m,相邻两支柱间的距离均为5m,将抛物线放在所给的直角坐标系中(如图2所示),拱桥的拱顶在y轴上.
(1)求拱桥所在抛物线的解析式;
(2)求支柱MN的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2米的隔离带),其中的一条行车道能否并排行驶宽2m、高2.4m的三辆汽车(隔离带与内侧汽车的间隔、汽车间的间隔、外侧汽车与拱桥的间隔均为0.5m)?请说说你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为﹣7,﹣1,3.乙袋中的三张卡片所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况.
(2)求点A落在第三象限的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列方程,属于一元一次方程的有( )
①x﹣2=
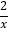 ;②0.5x=1;③
;②0.5x=1;③ =8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.
=8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
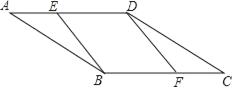
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
相关试题

