【题目】解不等式组
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式维的解集为 .
参考答案:
【答案】(1)x≥-1;(2)x>-2;(3)见详解 ;(4))x≥-1
【解析】
(1)去分母、移项、合并同类项、系数化为1,即可求解;
(2)去括号、移项、系数化为1,即可求解;
(3)把(1)和(2)求得的解集在数轴上表示出来;
(4)两个解集的公共部分就是不等式组的解集.
解:(1)不等式两边都乘以6,得 6+3+15x≥4x-2
移项,得 15x-4x≥-2-6-3
合并同类项,得 11x≥-11,
系数化为1,得 x≥-1
故答案为:x≥-1
(2)去括号,得 -3x-6<2x+4
移项,得 -3x-2x<4+6
合并同类项,得 -5x<10
系数化为1,得 x>-2
故答案为:x>-2
(3)在数轴上表示不等式的解集为:

(4)原不等式组的解集为:x≥-1.
故答案为:x≥-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于任何数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[-1.5]=-2.
(1)[-π]= ;
(2)如果[a]=2,那么a的取值范围是 ;
(3)如果[
 ]=-5,求满足条件的所有整数x;
]=-5,求满足条件的所有整数x;(4)直接写出方程6x-3[x]+7=0的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).

(1)将△ABC绕点B顺时针旋转90°得到△A′BC′,请画出△A′BC′.
(2)求BA边旋转到BA′位置时所扫过图形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】对任意有理数x,用[x]表示不大于x的最大整数.例如:[1.3]=1,[3]=3,[﹣2.5]=﹣3.以下结论正确的是_____.(把你认为正确结论的序号都填上)
①[﹣3.14]=﹣4;
②﹣[﹣x]=[x];
③[2x]=2[x];
④若[
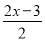 ]=﹣4,则x的取值范围是﹣
]=﹣4,则x的取值范围是﹣ ≤x<﹣
≤x<﹣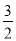 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为 ;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B',补全△A′B′C′;
(3)在图中画出△ABC的高CD;
(4)能使S△ABC=S△QBC的格点Q(A点除外)共有 个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市投入1380元资金购进甲、乙两种矿泉水共50箱,矿泉水的成本价和销售价如表所示:
类别/单价
成本价(元/箱)
销售价(元/箱)
甲
24
36
乙
33
48
(1)该超市购进甲、乙两种矿泉水各多少箱?
(2)全部售完50箱矿泉水,该超市共获得利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1的解析式为
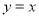 ,直线l2的解析式为
,直线l2的解析式为 ,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.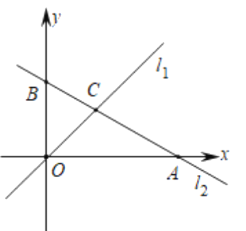

(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;
(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
相关试题

