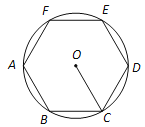
【题目】(1)如图1,在圆内接正六边形ABCDEF中,半径OC=4.求正六边形的边长.
(2)如图2,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求证:AB=AC.
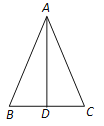
参考答案:
【答案】(1)4(2)证明见解析
【解析】试题分析:(1)连接OD,易证△OCD是等边三角形,即可得CD=OC=4,即正六边形的边长为4;(2)已知AD是△ABC的中线,可得BD=CD==5,由勾股定理的逆定理可得AD⊥BC,再由勾股定理求得AC=13,即可得AB=AC.
试题解析:
(1)连接OD,
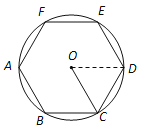
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠O=![]() ,
,
又∵OC=OD,
∴△OCD是等边三角形,
∴CD=OC=4,
即正六边形的边长为4.
(2)∵AD是△ABC的中线,
∴BD=CD= ![]() =5,
=5,
∵AB=13,AD=12,
∴BD2+AD2=52+122=169=132=AB2,
∴AD⊥BC,
∴AC2= CD2+AD2=52+122=169,
∴AC=13,
∴AB=AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别AB和CD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为( )

A.2
B.
C.
D.15 -
科目: 来源: 题型:
查看答案和解析>>【题目】小华通过学习函数发现:若二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,y1),(x2,y2) (x1 <x2),若y1y2<0,则方程ax2+bx+c=0(a≠0)的一个根x0的取值范围是x1<x0<x2,请你类比此方法推断方程x3+x-1=0的实数根x0所在范围为
A.
 B.
B.  C.
C.  D.
D. 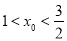
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)化简:5x+(2x+y)﹣(x﹣4y).
(2)先化简,再求值:(2x2﹣1+x)﹣2(x﹣x2﹣3),其中x=﹣ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.

(1)求证:DE=DF;
(2)求证:AE∥BD;
(3)求tan∠ACE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品进价为a元,商店将价格提高30%作零售价销售.在销售旺季过后,商店又以8折(即售价的80%)的价格开展促销活动.这时一件该商品的售价为( )
A.a元
B.0.8a元
C.1.04a元
D.0.92a元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:M=x3﹣3xy+2x+1,N=﹣3x+xy,求多项式3M+2N,并计算当x=﹣1,y=
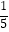 时,3M+2N的值.
时,3M+2N的值.
相关试题

