【题目】在平行四边形ABCD中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别AB和CD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为( ) 
A.2
B.![]()
C.![]()
D.15
参考答案:
【答案】C
【解析】解:设平行四边形ABCD的面积是S,设AB=5a,BC=3b.AB边上的高是3x,BC边上的高是5y. 则S=5a3x=3b5y.即ax=by= ![]() .
.
△AA4D2与△B2CC4全等,B2C= ![]() BC=b,B2C边上的高是
BC=b,B2C边上的高是 ![]() 5y=4y.
5y=4y.
则△AA4D2和△B2CC4的面积是2by= ![]() .
.
同理△D2C4D与△A4BB2的面积是 ![]() .
.
则四边形A4B2C4D2的面积是S﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ,即
,即 ![]() =1,
=1,
解得S= ![]() .
.
故选C.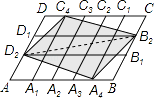
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个物体的俯视图是圆,则该物体的形状是( )
A. 球体B. 圆柱C. 圆锥D. 以上都有可能
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.
(1)该市的养老床位数从
 年底的
年底的 万个增长到
万个增长到 年底的
年底的 万个,求该市这两年(从
万个,求该市这两年(从 年底到
年底到 年底)拥有的养老床位数的平均年增长率;
年底)拥有的养老床位数的平均年增长率;(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共
 间,这三类养老专用房间分别为单人间(
间,这三类养老专用房间分别为单人间( 个养老床位),双人间(
个养老床位),双人间( 个养老床位),三人间(
个养老床位),三人间( 个养老床位),因实际需要,单人间房间数在
个养老床位),因实际需要,单人间房间数在 至
至 之间(包括
之间(包括 和
和 ),且双人间的房间数是单人间的
),且双人间的房间数是单人间的 倍,设规划建造单人间的房间数为
倍,设规划建造单人间的房间数为 .
.①若该养老中心建成后可提供养老床位
 个,求
个,求 的值;
的值;②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )

A.24 B.12 C.6 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华通过学习函数发现:若二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,y1),(x2,y2) (x1 <x2),若y1y2<0,则方程ax2+bx+c=0(a≠0)的一个根x0的取值范围是x1<x0<x2,请你类比此方法推断方程x3+x-1=0的实数根x0所在范围为
A.
 B.
B.  C.
C.  D.
D. 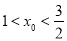
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)化简:5x+(2x+y)﹣(x﹣4y).
(2)先化简,再求值:(2x2﹣1+x)﹣2(x﹣x2﹣3),其中x=﹣ .
. -
科目: 来源: 题型:
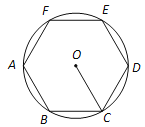
查看答案和解析>>【题目】(1)如图1,在圆内接正六边形ABCDEF中,半径OC=4.求正六边形的边长.
(2)如图2,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求证:AB=AC.
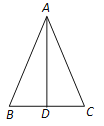
相关试题

