【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖. 
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?
参考答案:
【答案】
(1)解:设操场四角的每个小正方形边长是x米,根据题意,
得:4x2+(100﹣2x)(80﹣2x)=4[2x(100﹣2x)+2x(80﹣2x)],
整理,得:x2﹣45x+200=0,
解得:x1=5,x2=40(舍去),
故操场四角的每个小正方形边长是5米
(2)解:设铺矩形广场地面的总费用为y元,广场四角的小正方形的边长为x米,
则,y=30×[4x2+(100﹣2x)(80﹣2x)]+20×[2x(100﹣2x)+2x(80﹣2x)]
即:y=80x2﹣3600x+240000
配方得,y=80(x﹣22.5)2+199500
当x=22.5时,y的值最小,最小值为19.95万元>15万元,
故这些资金不能购买所需的全部地面砖,教育局还应该至少给学校解决19.95﹣15=4.95万元资金.
【解析】(1)设小正方形的边长为x米,表示出里边大矩形的长为(100﹣2x)米,宽为(80﹣2x)米,利用灰色部分的面积=4个小正方形的面积+里边大矩形的面积,红色部分面积=上下两个矩形面积+左右两个矩形面积,根据灰色地面砖的面积是铺红色地面砖面积的4倍列出关于x的方程,求出方程的解得到x的值,即为小正方形的边长;(2)设铺矩形广场地面的总费用为y元,广场四角的小正方形的边长为x米,根据等量关系“总费用=铺白色地面砖的费用+铺绿色地面砖的费用”列出y关于x的函数,求得最小值,与15万元比较可得是否够用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=
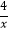 的图象经过点B;反比例函数y2=
的图象经过点B;反比例函数y2= 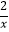 的图象经过点C(
的图象经过点C( 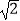 ,m).
,m).
(1)求点B的坐标;
(2)△ABC的内切圆⊙M与BC,CA,AB分别相切于D,E,F,求圆心M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CB,AD=CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E、F.求证:OE=OF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD上的点.且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;

探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=
 ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离?
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O是△ABC的外接圆,AB是直径,过
 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2 ,求AC的长.
,求AC的长. 
-
科目: 来源: 题型:
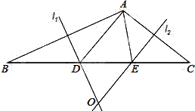
查看答案和解析>>【题目】如图,在△ABC中,AB边的垂直平分线
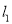 交BC于D,AC边的垂直平分线
交BC于D,AC边的垂直平分线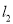 交BC于E,
交BC于E, 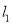 与
与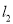 相交于点O,△ADE的周长为6cm.
相交于点O,△ADE的周长为6cm.(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是_________.

相关试题

