【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求AD:EF的值.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)由线段垂直平分线的性质得出GA=GB,GD=GC,由SAS证明△AGD≌△BGC,得出对应边相等即可;
(2)先证出∠AGB=∠DGC,由![]() ,证出△AGB∽△DGC,得出比例式
,证出△AGB∽△DGC,得出比例式![]() ,再证出∠AGD=∠EGF,即可得出△AGD∽△EGF;
,再证出∠AGD=∠EGF,即可得出△AGD∽△EGF;
(3)延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH,由△AGD≌△BGC,得出∠GAD=∠GBC,再求出∠AGB=∠AHB=90°,得出∠AGE=![]() ∠AGB=45°,求出
∠AGB=45°,求出![]() ,由△AGD∽△EGF,即可得出
,由△AGD∽△EGF,即可得出![]() 的值.
的值.
试题解析:(1)证明:∵GE是AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
 ,
,
∴△AGD≌△BGC(SAS),
∴AD=BC;
(2)证明:∵∠AGD=∠BGC,
∴∠AGB=∠DGC,
在△AGB和△DGC中, ![]() ,
,
∴△AGB∽△DGC,
∴![]() ,
,
又∵∠AGE=∠DGF,
∴∠AGD=∠EGF,
∴△AGD∽△EGF;
(3)延长AD交GB于点M,交BC的延长线于点H,如图所示:
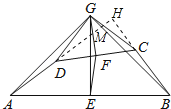
则AH⊥BH,
∵△AGD≌△BGC,
∴∠GAD=∠GBC,
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,
∴∠AGB=∠AHB=90°,
∴∠AGE=![]() ∠AGB=45°,
∠AGB=45°,
∴![]() ,
,
又∵△AGD∽△EGF,
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为直角三角形,∠ACB=900,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;
(3)设点Q为抛物线上点P至点B之间的一动点,连结PQ并延长交BC于点E,连结BQ并延长交AC于点F,试证明:FC(AC+BC)为定值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.

(1)求AB的长;
(2)△ABC的形状是三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.

(1)求证:CD是⊙O的切线;
(2)过点B作O的切线,交CD的延长线于点E,若BC=12,tan∠CDA=
 ,求BE的长.
,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校体育社团在校内开展“最喜欢的体育项目(四项选一项)”调查,对九年级学生随机抽样,并将收集的数据绘制成如图两幅不完整的统计图,请结合统计图解答下列问题:

(1)求本次抽样人数有多少人?
(2)补全条形统计图;
(3)该校九年级共有600名学生,估计九年级最喜欢跳绳项目的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种零件的直径规格是20±0.2mm,经检查,一个零件的直径18mm,该零件____________(填“合格”或“不合格”);
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,且DE∥BF,分别交对角线AC于点E、F,连接EB,FD.

求证:BE∥DF.
相关试题

