Question

【题目】如图，已知△ABC为直角三角形，∠ACB=900，AC=BC,点A、C在x轴上，点B坐标为(3，m)（m>0），线段AB与y轴相交于点D，以P（1，0）为顶点的抛物线过点B、D．

（1）求点A的坐标（用m表示）；

（2）求抛物线的解析式；

（3）设点Q为抛物线上点P至点B之间的一动点，连结PQ并延长交BC于点E，连结BQ并延长交AC于点F，试证明：FC(AC+BC)为定值．

Answer 1

【答案】（1）（）；（2）；（3）见解析.

【解析】试题分析：（1）AO=AC-OC=m-3，用线段的长度表示点A的坐标；（2）∵△ABC是等腰直角三角形，∴△AOD也是等腰直角三角形，∴OD=OA，∴D（0，m-3），又P（1，0）为抛物线顶点，可设顶点式，求解析式；（3）设Q（x，x2-2x+1），过Q点分别作x轴，y轴的垂线，运用相似比求出FC、EC的长，而AC=m，代入即可．

试题解析：（1） 由B（3，m）可知OC=3，BC=m，

又△ABC为等腰直角三角形，

∴AC=BC=m，OA=m-3，

∴点A的坐标是（3-m，0）．

（2）∵∠ODA=∠OAD=45°

∴OD=OA=m-3，

则点D的坐标是（0，m-3）．

又抛物线顶点为P（1，0），且过点B、D，

所以可设抛物线的解析式为：y=a（x-1）2，

得：

解得

∴抛物线的解析式为y=x2-2x+1；

（3）证明：过点Q作QM⊥AC于点M，过点Q作QN⊥BC于点N，

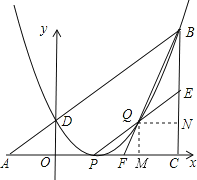
设点Q的坐标是（x，x2-2x+1），

则QM=CN=（x-1）2，MC=QN=3-x．

∵QM∥CE

∴△PQM∽△PEC

∴

即，得EC=2（x-1）

∵QN∥FC

∴△BQN∽△BFC

∴，

即，得FC=

又∵AC=4

∴FC（AC+EC）= [4+2（x-1）]= （2x+2）=×2×（x+1）=8

即FC（AC+EC）为定值8．