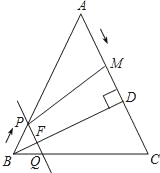
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为y(cm2),求y与t之间的函数关系式.
参考答案:
【答案】(1)当t=![]() s时,四边形PQCM是平行四边形;(2)y=
s时,四边形PQCM是平行四边形;(2)y=![]() t2﹣8t+40.
t2﹣8t+40.
【解析】试题分析:(1)假设![]() 为平行四边形,根据平行四边形的性质得到对边平行,进而得到AP=AM,列出关于t的方程,求出方程的解得到满足题意t的值;
为平行四边形,根据平行四边形的性质得到对边平行,进而得到AP=AM,列出关于t的方程,求出方程的解得到满足题意t的值;
(2)根据![]() ,可得△PBQ∽△ABC,根据相似三角形的形状必然相同可知
,可得△PBQ∽△ABC,根据相似三角形的形状必然相同可知![]() 也为等腰三角形,即
也为等腰三角形,即![]() 再由证得的相似三角形得底比底等于高比高,用含
再由证得的相似三角形得底比底等于高比高,用含![]() 的代数式就可以表示出
的代数式就可以表示出![]() ,进而得到梯形的高
,进而得到梯形的高![]() 又点
又点![]() 的运动速度和时间可知点
的运动速度和时间可知点![]() 走过的路程
走过的路程![]() 所以梯形的下底
所以梯形的下底![]() 最后根据梯形的面积公式即可得到
最后根据梯形的面积公式即可得到![]() 与
与![]() 的关系式;
的关系式;
试题解析:(1)假设四边形PQCM是平行四边形,则PM∥QC,
∴AP:AB=AM:AC,
∵AB=AC,
∴AP=AM,即10t=2t,
解得: ![]()
∴当![]() 时,四边形PQCM是平行四边形;
时,四边形PQCM是平行四边形;
(2)∵![]() ,
,
∴△PBQ∽△ABC,
∴△PBQ为等腰三角形,PQ=PB=t,
∴![]() ,即
,即![]()
解得: ![]()
![]()
又∵![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段

求作:菱形
 ,使得
,使得 且
且 .
.以下是小丁同学的作法:
①作线段
 ;
;②分别以点
 ,
, 为圆心,线段
为圆心,线段 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点 ;
;③再分别以点
 ,
, 为圆心,线段
为圆心,线段 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点 ;
;④连接
 ,
, ,
, .
.则四边形
 即为所求作的菱形.(如图)
即为所求作的菱形.(如图)老师说小丁同学的作图正确.则小丁同学的作图依据是:_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠D应分别是20°和30°.
(1)李叔叔量得∠BCD=142°,根据李叔叔量得的结果,你能断定这个零件是否合格?请解释你的结论.
(2)你知道∠B、∠D、∠BCD三角之间有何关系吗?请写出你的结论(不需说明理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们已经学过用尺规作一条线段等于已知线段、作一个角等于已知角.请同学们看下面一个尺规作图的例子:
①以O为圆心,任意长为半径作弧线交∠AOB的两边OA、OB分别于C、D两点;
②以C为圆心,大于
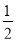 CD的长为半径作弧线,再以D为圆心,同样的长为半径作弧线,两弧线交于P点;
CD的长为半径作弧线,再以D为圆心,同样的长为半径作弧线,两弧线交于P点;③以O为端点作射线OP.
则OP就是∠AOB的平分线
你知道OP为什么是∠AOB的角平分线吗?请用你所学的知识解释.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.

(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
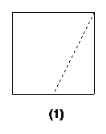
查看答案和解析>>【题目】(1)如图(1),在正方形一边上取中点,并沿虚线剪开,用两块图形拼一拼,能否拼出平行四边形、梯形或三角形?画图解释你的判断.
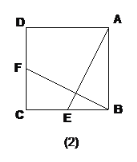
(2)如图(2)E为正方形ABCD边BC的中点,F为DC的中点,BF与AE有何关系?请解释你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).


请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
相关试题

