Question

【题目】如图，在△ABC中，AB=AC，AD是BC边上的中线，以AD为直径作⊙O，连接BO并延长至点E，使得OE=OB，交⊙O于点F，连接AE，CE．
（1）求证：AE是⊙O的切线；
（2）求证：四边形ADCE是矩形；
（3）若BD= AD=4，求阴影部分的面积．

Answer 1

【答案】
（1）证明：∵AB=AC，AD是BC边上的中线，

∴∠ODB=90°，

在△BOD和△EOA中，

，

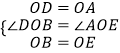∴△BOD≌△EOA，

∴∠OAE=∠ODB=90°，

∵点A在圆上，

∴AE是⊙O的切线；

（2）由（1）知，△BOD≌△EOA，

∴BD=AE，

∵AD是BC边上的中线，

∴CD=BD，

∴AE=CD，

∵∠OAE=∠ODB=90°，

∴AE∥BC，

∴四边形ADCE是平行四边形

∵∠OAE=90°，

∴平行四边形ADCE是矩形；

（3）解：∵∠ODB=90°，BD=OD，

∴∠BOD=45°，

∴∠AOE=45°

∵∠OAE=90°，

∴AE=OA= AD=4

∴S△OAE= ×OA×AE= ×4×4=8，

S扇形OAF=π×42× =2π，

∴S阴影部分=S△OAE﹣S扇形OAF=8﹣2π．

【解析】（1）利用等腰三角形的三线合一的性质，得出∠ODB=90°，从而得出△BOD≌△EOA，得出∠OAE=∠ODB=90°，即可；（2）利用（1）△BOD≌△EOA和三角形的中线得出结论；（3）先判断出AE=OA=4，阴影部分面积用三角形OAE的面积减去扇形OAF的面积即可．