【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上。
(1)如果点P在C、D之间运动时,试说明∠1+∠3=∠2;
(2)如果点P在直线l1的上方运动时,试探索∠1,∠2,∠3之间的关系又是如何?
(3)如果点P在直线l2的下方运动时,试探索∠PAC,∠PBD,∠APB之间的关系又是如何? (直接写出结论)

参考答案:
【答案】(1)证明见解析(2)当点P在线段DC的延长线上时,∠2=∠3-∠1(3)∠APB+∠PBD=∠PAC
【解析】分析:(1)过点P作PE∥l1,根据l1∥l2可知PE∥l2,根据平行线的性质可得出∠1=∠APE,∠3=∠BPE.再由∠2=∠APE+∠BPE即可得出结论;
(2)如图2所示,当点P在直线l1的上方运动时,∠2=∠3-∠1,过点P作PF∥l1,根据l1∥l2可知PE∥l2,根据平行线的性质可得出∠FPA=∠1,∠FPB=∠3, 即可得∠2=∠FPB-∠PFA=∠3-∠1;(3)∠APB+∠PBD=∠PAC,类比(2)的方法证明即可.
详解:
(1)证明:如图1,过点P作PE∥l1,
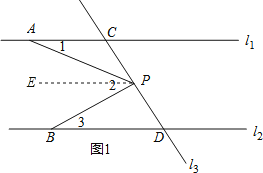
∵l1∥l2,
∴PE∥l2,
∴∠1=∠APE,∠3=∠BPE.
又∵∠2=∠APE+∠BPE,
∴∠2=∠1+∠3;
(2)如图2所示,当点P在直线l1的上方运动时,∠2=∠3-∠1.
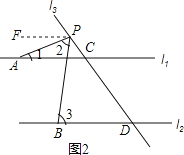
理由:过点P作PF∥l1,
∠FPA=∠1.
∵l1∥l2,
∴PF∥l2,
∴∠FPB=∠3,
∴∠2=∠FPB-∠PFA=∠3-∠1;
(3)∠APB+∠PBD=∠PAC,
理由:如图3所示,点P在直线l2的下方运动时,∠APB+∠PBD=∠PAC.
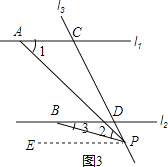
理由:过点P作PE∥l2,∠EPB=∠3.
∵l1∥l2,
∴PE∥l1,
∴∠EPA=∠1,
∴∠2=∠EPA-∠EPB=∠1-∠3.
即∠APB+∠PBD=∠PAC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE∥BF,AC平分∠BAE,交BF于C.
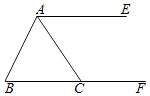
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)在(1)的图形中,找出两条相等的线段,并予以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列诗句所描述的事件中,是不可能事件的是( )
A. 黄河入海流 B. 锄禾日当午 C. 大漠孤烟直 D. 手可摘星辰
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象交于A(﹣3,2),B(2,n).
(k≠0)的图象交于A(﹣3,2),B(2,n). 
(1)求反比例函数y= 的解析式;
的解析式;
(2)求一次函数y=ax+b的解析式;
(3)观察图象,直接写出不等式ax+b< 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+| b-3|=0,线段AB交y轴于F点.
(1)求点A、B的坐标.
(2)求点F的坐标;
(3)点P为坐标轴上一点,若△ABP的面积和△ABC的面积相等,求出P点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整).

分数(分)
人数(人)
68
4
78
7
80
3
88
5
90
10
96
6
100
5
(1)补全条形统计图;
(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;
(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?
(4)小明的成绩为88分,他的成绩如何,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)求出S△ABC
 (3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标。
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标。
相关试题

