【题目】如图1,在直角坐标系中,O是坐标原点,点A在y轴正半轴上,二次函数y=ax2+ ![]() x+c的图象F交x轴于B、C两点,交y轴于M点,其中B(﹣3,0),M(0,﹣1).已知AM=BC.
x+c的图象F交x轴于B、C两点,交y轴于M点,其中B(﹣3,0),M(0,﹣1).已知AM=BC.
(1)求二次函数的解析式;
(2)证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;
(3)在(2)的条件下,设直线l过D且分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N.
①若直线l⊥BD,如图1,试求 ![]() 的值;
的值;
②若l为满足条件的任意直线.如图2.①中的结论还成立吗?若成立,证明你的猜想;若不成立,请举出反例.
参考答案:
【答案】
(1)
解:∵二次函数y=ax2+ ![]() x+c的图象经过点B(﹣3,0),M(0,﹣1),
x+c的图象经过点B(﹣3,0),M(0,﹣1),
∴ 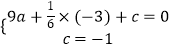 ,
,
解得a= ![]() ,c=﹣1.
,c=﹣1.
∴二次函数的解析式为:y= ![]() x2+
x2+ ![]() x﹣1
x﹣1
(2)
解:由二次函数的解析式为:y= ![]() x2+
x2+ ![]() x﹣1,
x﹣1,
令y=0,得 ![]() x2+
x2+ ![]() x﹣1=0,
x﹣1=0,
解得x1=﹣3,x2=2,∴C(2,0),∴BC=5;
令x=0,得y=﹣1,∴M(0,﹣1),OM=1.
又AM=BC,∴OA=AM﹣OM=4,∴A(0,4).
设AD∥x轴,交抛物线于点D,如图1所示,
则yD= ![]() x2+
x2+ ![]() x﹣1=OA=4,
x﹣1=OA=4,
解得x1=5,x2=﹣6(位于第二象限,舍去)
∴D点坐标为(5,4).
∴AD=BC=5,
又∵AD∥BC,
∴四边形ABCD为平行四边形.
即在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形.
设直线BD解析式为:y=kx+b,∵B(﹣3,0),D(5,4),
∴ ![]() ,
,
解得:k= ![]() ,b=
,b= ![]() ,
,
∴直线BD解析式为:y= ![]() x+
x+ ![]()
(3)
解:在Rt△AOB中,AB= ![]() =5,又AD=BC=5,∴ABCD是菱形.
=5,又AD=BC=5,∴ABCD是菱形.
①若直线l⊥BD,如图1所示.
∵四边形ABCD是菱形,
∴AC⊥BD,
∴AC∥直线l,
∴ ![]() ,
,
∵BA=BC=5,
∴BP=BQ=10,
∴ ![]() =
= ![]() =
= ![]() ;
;
②若l为满足条件的任意直线,如图2所示,此时①中的结论依然成立,理由如下:
∵AD∥BC,CD∥AB,
∴△PAD∽△DCQ,
∴ ![]() ,∴APCQ=ADCD=5×5=25.
,∴APCQ=ADCD=5×5=25.
∴ ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]() .
.
【解析】(1)利用待定系数法求出二次函数的解析式;(2)首先求出D点的坐标,可得AD=BC且AD∥BC,所以四边形ABCD是平行四边形;再根据B、D点的坐标,利用待定系数法求出直线BD的解析式;(3)本问的关键是判定平行四边形ABCD是菱形.①推出AC∥直线l,从而根据平行线间的比例线段关系,求出BP、CQ的长度,计算出 ![]() =
= ![]() ;②判定△PAD∽△DCQ,得到APCQ=25,利用这个关系式对
;②判定△PAD∽△DCQ,得到APCQ=25,利用这个关系式对 ![]() 进行分式的化简求值,结论为
进行分式的化简求值,结论为 ![]() =
= ![]() 不变.
不变.
【考点精析】通过灵活运用平行四边形的判定与性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个命题:①一个多边形的内角和为900°,从这个多边形同一个顶点可画的对角线有4条;②三角形的三条高所在的直线的交点可能在三角形的内部或外部;③多边形的所有内角中最多有3个锐角;④△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形.其中真命题的是_______________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为______;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系是______;
(4)在图中画出△ABC的高CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择. 方案一:每千克种子价格为4元,无论购买多少均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次性购买超过3千克的,则超过3千克的部分的种子价格打7折.
(1)请分别求出方案一和方案二中购买的种子数量x(千克)和付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.
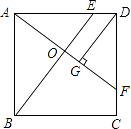
(1)求证:AF⊥BE;
(2)试探究线段AO、BO、GO的长度之间的数量关系;
(3)若GO:CF=4:5,试确定E点的位置. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数称为“和谐数”.例如:自然数12321,从最高位到个位排出的一串数字是:1,2,3,2,1,从个位到最高排出的一串数字仍是:1,2,3,2,1,因此12321是一个“和谐数”.再如:22,545,3883,34543,…,都是“和谐数”.
(1)请你直接写出3个四位“和谐数”;请你猜想任意一个四位“和谐数”能否被11整除,并说明理由;
(2)已知一个能被11整除的三位“和谐数”,设其个位上的数字为x(
 ,x为自然数),十位上的数字为y,求y与x的函数关系式.
,x为自然数),十位上的数字为y,求y与x的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:
(2)解不等式组: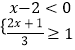 .
.
相关试题

