【题目】如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC. 
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
参考答案:
【答案】
(1)解:∵A(﹣1,0)、B(3,0),
∴AO=1,OB=3,即AB=AO+OB=1+3=4.
∴OC=4,即点C的坐标为(0,4)
(2)解:设图象经过A、C、B三点的二次函数的解析式为y=ax2+bx+c,把A、C、B三点的坐标分别代入上式,
得  ,
,
解得a=﹣ ![]() ,b=
,b= ![]() x,c=4,
x,c=4,
∴所求的二次函数解析式为y=﹣ ![]() x2+
x2+ ![]() x+4.
x+4.
∵点A、B的坐标分别为点A(﹣1,0)、B(3,0),
∴线段AB的中点坐标为(1,0),即抛物线的对称轴为直线x=1.
∵a=﹣ ![]() <0,
<0,
∴当x=1时,y有最大值y=﹣ ![]() +
+ ![]() +4=
+4= ![]()
【解析】(1)首先求得AB,得出OC,求得点C的坐标;(2)利用待定系数法求的函数解析式,进一步利用顶点坐标公式求得最值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1 .
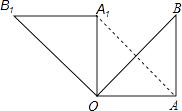
(1)线段OA1的长是 , ∠AOB1的度数是;
(2)连接AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求点B旋转到点B1的位置所经过的路线的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.

(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论
①a>0,②b>0,③c>0,④b2﹣4ac>0
其中正确的有( )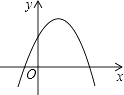
A.1个
B.2个
C.3个
D.4个
相关试题

