【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论
①a>0,②b>0,③c>0,④b2﹣4ac>0
其中正确的有( )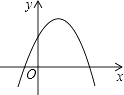
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:①∵该二次函数图象的开口方向向下,
∴a<0;
故本选项错误;
②∵该图象的对称轴x=﹣ ![]() >0,
>0,
∴b>0;
故本选项正确;
③∵该函数图象与y轴交于正半轴,
∴c>0;
故本选项正确;
④该二次函数的图象与x轴有2个不相同的交点,依据根的判别式可知b2﹣4ac>0;
故本选项正确;
综上所述,正确的说法是:②③④,共有3个;
故选C.
【考点精析】认真审题,首先需要了解二次函数图象以及系数a、b、c的关系(二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.

(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1 .
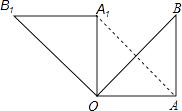
(1)线段OA1的长是 , ∠AOB1的度数是;
(2)连接AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求点B旋转到点B1的位置所经过的路线的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.

(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形
 的顶点
的顶点 的坐标为
的坐标为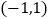 ,点
,点 在
在 轴正半轴上,点
轴正半轴上,点 在第三象限的双曲线
在第三象限的双曲线 上,过点
上,过点 作
作 轴交双曲线于点
轴交双曲线于点 ,连接
,连接 ,则
,则 的面积为__________.
的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市在城市建设中,要折除旧烟囱AB(如图所示),在烟囱正西方向的楼CD的顶端C,测得烟囱的顶端A的仰角为45°,底端B的俯角为30°,已量得DB=21m.
(1)在原图上画出点C望点A的仰角和点C望点B的俯角,并分别标出仰角和俯角的大小;
(2)拆除时若让烟囱向正东倒下,试问:距离烟囱正东35m远的一棵大树是否被歪倒的烟囱砸着?请说明理由.(
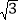 ≈1.732)
≈1.732)
相关试题

