【题目】如图所示,以△ABC的两边AB、AC为边向外作等边△ABD和等边△ACE,DC、BE相交于点O.
(1)求证:DC=BE;
(2)求∠BOC的度数;
(3)当∠BAC的度数发生变化时,∠BOC的度数是否变化?若不变化,请求出∠BOC的度数;若发生变化,请说明理由.

参考答案:
【答案】(1)证明见解析; (2)∠BOC=120°;(3)当∠BAC的度数发生变化时,∠BOC的度数不变.∠BOC=120°.
【解析】
(1)易证∠DAB=∠EAC=60°,AD=AB,AE=AC,即可求得∠DAC=∠BAE,即可证明△DAC≌△BAE;
(2)根据(1)中结论可得∠ADC=∠ABE,即可求得∠ODB+∠OBD=∠ADB+∠ABD,根据三角形外角性质即可解题;
(3)由(2)可得∠ODB+∠OBD=∠ADB+∠ABD,因此可以判定∠BOC和∠BAC大小无关.
(1)证明:∵△ADB和△AEC都是等边三角形,
∴∠DAB=∠EAC=60°,AD=AB,AE=AC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
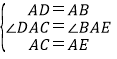 ,
,
∴△DAC≌△BAE(SAS);
∴DC=BE
(2)解:∵△DAC≌△BAE,
∴∠ADC=∠ABE,
∴∠ODB+∠OBD=∠ADB-∠ADC+∠ABD+∠ABE=∠ADB+∠ABD=120°,
∴∠BOC=∠ODB+∠OBD=120°,
(3)解:∵由(2)可得∠ODB+∠OBD=∠ADB+∠ABD,
∴∠BOC和∠BAC大小无关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下图,回答问题.
(1)反映了哪两个变量之间的关系?
(2)点A,B分别表示什么?
(3)说一说速度是怎样随时间变化而变化的;
(4)你能找到一个实际情境,大致符合下图所刻画的关系吗?
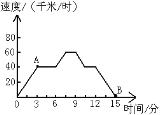
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的
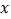 值为
值为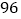 ,我们发现第
,我们发现第 次输出的结果为
次输出的结果为 ,第
,第 次输出的结果为
次输出的结果为 ,……第
,……第 次输出的结果_______________;第
次输出的结果_______________;第 次输出的结果为______________.
次输出的结果为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平整的桌面上,有若干个棱长为
 的小正方体堆成一个几何体,如图所示
的小正方体堆成一个几何体,如图所示
(1)分别画出这个几何体从上面、左面看到的图形;
(2)如果把露在外面的面都涂上颜色,求涂上颜色的面的面积;
(3)若你手里还有一些相同的小正方体,如果保持从上面、左面看到的图形不变,最多可以再添加几个小正方体?直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=﹣x2+6x﹣9的图象顶点为A,与y轴交于点B.若在该二次函数图形上取一点C,在x轴上取一点D,使得四边形ABCD为平行四边形,则D点的坐标为( )
A.(﹣9,0)
B.(﹣6,0)
C.(6,0)
D.(9,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解七年级男生体质健康情况,随机抽取若干名男生进行测试,测试结果分为优秀、良好、合格、不合格四个等级,统计整理数据并绘制图1、图2两幅不完整的统计图,请根据图中信息回答下列问题:

(1)本次接收随机抽样调查的男生人数为人,扇形统计图中“良好”所对应的圆心角的度数为;
(2)补全条形统计图中“优秀”的空缺部分;
(3)若该校七年级共有男生480人,请估计全年级男生体质健康状况达到“良好”的人数.
相关试题

