【题目】找规律
(1)先阅读,再填空: (x+5)(x+6)=x2+11x+30;
(x﹣5)(x﹣6)=x2﹣11x+30;
(x﹣5)(x+6)=x2+x﹣30;
(x+5)(x﹣6)=x2﹣x﹣30.
观察上面的算式,根据规律,直接写出下列各式的结果:
(a+90)(a﹣100)=; (y﹣80)(y﹣90)= .
(2)先阅读,再填空:(x﹣1)(x+1)=x2﹣1;(x﹣1)(x2+x+1)=x3﹣1;(x﹣1)(x3+x2+x+1)=x4﹣1;(x﹣1)(x4+x3+x2+x+1)=x5﹣1. 观察上面各式:①由此归纳出一般性规律:(x﹣1)(xn﹣1+xn﹣2+xn﹣3+…+x2+x+1)=;
②根据①直接写出1+3+32+…+367+368的结果 .
参考答案:
【答案】
(1)a2﹣10a﹣9000;y2﹣170y+7200
(2)xn﹣1;![]()
【解析】解:(1)∵(x+5)(x+6)=x2+(5+6)x+5×6=x2+11x+30; (x﹣5)(x﹣6)=x2+(﹣5﹣6)x+(﹣5)×(﹣6)=x2﹣11x+30;
(x﹣5)(x+6)=x2+(﹣5+6)x+(﹣5)×6=x2+x﹣30;
(x+5)(x﹣6)=x2+(5﹣6)x+5×(﹣6)=x2﹣x﹣30,
∴(a+90)(a﹣100)=a2+(90﹣100)a+90×(﹣100)=a2﹣10a﹣9000,
(y﹣80)(y﹣90)=y2+(﹣80﹣90)y+(﹣80)×(﹣90)=y2﹣170y+7200,
所以答案是:a2﹣10a﹣9000,y2﹣170y+7200.
2)①由题意知,(x﹣1)(xn﹣1+xn﹣2+xn﹣3+…+x2+x+1)=xn﹣1,
所以答案是:xn﹣1;
②原式= ![]() ×(3﹣1)×(1+3+32+…+367+368)=
×(3﹣1)×(1+3+32+…+367+368)= ![]() ×(369﹣1),
×(369﹣1),
所以答案是: ![]() .
.
【考点精析】本题主要考查了有理数的四则混合运算的相关知识点,需要掌握在没有括号的不同级运算中,先算乘方再算乘除,最后算加减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题:
AQI指数
质量等级
天数(天)
0﹣50
优
m
51﹣100
良
44
101﹣150
轻度污染
n
151﹣200
中度污染
4
201﹣300
重度污染
2
300以上
严重污染
2
(1 )统计表中m= ,n= .扇形统计图中,空气质量等级为“良”的天数占 %;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少天?
(3)据调查,严重污染的2天发生在春节期间,燃放烟花爆竹成为空气污染的一个重要原因,据此,请你提出一条合理化建议.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道a+b=0时,a3+b3=0也成立,若将a看成a3的立方根,b看成b3的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数.
(1)试举一个例子来判断上述猜测结论是否成立;
(2)若 与
与  互为相反数,求
互为相反数,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程为( )
A.2(1+x)2=8B.2(1﹣x)2=8
C.2+2(1+x)+2(1+x)2=8D.2(1+x)+2(1+x)2=8
-
科目: 来源: 题型:
查看答案和解析>>【题目】去年,汶川地区发生特大地震,造成当地重大经济损失,在“情系灾区”捐款活动中,某同学对甲、乙两班情况进行统计,得到三条信息:
①甲班共捐款300元,乙班共捐232元;
②甲班比乙班多2人;
③乙班平均每人捐款数是甲班平均每人捐款数的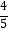 ;
;
请你根据以上信息,求出甲班平均每人捐款多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】y=-x+1经过的象限是( )
A.一、三B.二、 四C.一、二、三D.一、二、四
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1200名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
 (1)这次抽取了多少名学生的竞赛成绩进行统计,m,n分别是多少?
(1)这次抽取了多少名学生的竞赛成绩进行统计,m,n分别是多少?(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
相关试题

