Question

【题目】某学校环保志愿者协会对该市城区的空气质量进行调查，从全年365天中随机抽取了80天的空气质量指数（AQI）数据，绘制出三幅不完整的统计图表．请根据图表中提供的信息解答下列问题：

AQI指数	质量等级	天数（天）
0﹣50	优	m
51﹣100	良	44
101﹣150	轻度污染	n
151﹣200	中度污染	4
201﹣300	重度污染	2
300以上	严重污染	2

（1 ）统计表中m= ，n= ．扇形统计图中，空气质量等级为“良”的天数占 %；

（2）补全条形统计图，并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少天？

（3）据调查，严重污染的2天发生在春节期间，燃放烟花爆竹成为空气污染的一个重要原因，据此，请你提出一条合理化建议．

Answer 1

【答案】(1)20，8，55；(2)292，统计图见解析；（3）提出合理建议，比如不燃放烟花爆竹或少燃放烟花爆竹等，合理即可.

【解析】

试题分析：（1）由A占25%，即可求得m的值，继而求得n的值，然后求得空气质量等级为“良”的天数占的百分比；（2）首先由（1）补全统计图，然后利用样本估计总体的知识求解即可求得答案；（3）提出合理建议，比如不燃放烟花爆竹或少燃放烟花爆竹等．

试题解析：解：（1）∵m=80×25%=20，n=80﹣20﹣44﹣4﹣2﹣2=8，

∴空气质量等级为“良”的天数占：×100%=55%．

（2）估计该市城区全年空气质量等级为“优”和“良”的天数共：365×（25%+55%）=292（天），

答：估计该市城区全年空气质量等级为“优”和“良”的天数共292天；

补全统计图：

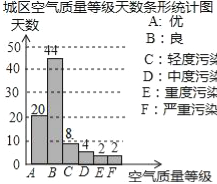
（3）建议不要燃放烟花爆竹．