【题目】如图,抛物线y=![]() ﹣x﹣4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
﹣x﹣4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
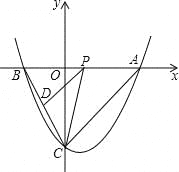
(1)直接写出A、B、C的坐标;
(2)求抛物线y=![]() ﹣x﹣4的对称轴和顶点坐标;
﹣x﹣4的对称轴和顶点坐标;
(3)求△PCD面积的最大值,并判断当△PCD的面积取最大值时,以PA、PD为邻边的平行四边形是否为菱形.
参考答案:
【答案】(1)A(4,0)、B(﹣2,0)、C(0,﹣4).(2)(1,﹣![]() )(3)不是菱形
)(3)不是菱形
【解析】试题分析:(1)设y=0,解一元二次方程即可求出A和B的坐标,设x=0,则可求出C的坐标.
(2)抛物线:y=![]() x2-x-4=
x2-x-4=![]() (x-1)2-
(x-1)2-![]() ,所以抛物线的对称轴是直线x=1,顶点坐标是(1,-
,所以抛物线的对称轴是直线x=1,顶点坐标是(1,-![]() ).
).
(3)设P(x,0)(-2<x<4),由PD∥AC,可得到关于PD的比例式,由此得到PD和x的关系,再求出C到PD的距离(即P到AC的距离),利用三角形的面积公式可得到S和x的函数关系,利用函数的性质即可求出三角形面积的最大值,进而得到x的值,所以PD可求,而PA≠PD,所以PA、PD为邻边的平行四边形不是菱形.
试题解析:(1)A(4,0)、B(-2,0)、C(0,-4).
(2)抛物线:y=![]() x2-x-4=
x2-x-4=![]() (x-1)2-
(x-1)2-![]() ,
,
∴抛物线的对称轴是直线x=1,顶点坐标是(1,-![]() ).
).
(3)设P(x,0)(-2<x<4),
∵PD∥AC,
∴![]() ,
,
解得:PD=![]() (x+2),
(x+2),
∵C到PD的距离(即P到AC的距离):d=PA×sin450=![]() (4-x),
(4-x),
∴△PCD的面积S=![]() ×PD×d=
×PD×d=![]() (x+2)(4-x)="-"
(x+2)(4-x)="-"![]() x2+
x2+![]() x+
x+![]() ,
,
∴S=-![]() (x-1)2+3,
(x-1)2+3,
∴△PCD面积的最大值为3,
当△PCD的面积取最大值时,x=1,PA=4-x=3,PD=![]() (x+2)=2
(x+2)=2![]() ,
,
因为PA≠PD,所以以PA、PD为邻边的平行四边形不是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式的值:
(1)( +
+  )﹣
)﹣ 
(2)(﹣3)2﹣|﹣ |+
|+  ﹣
﹣ 
(3)x2﹣121=0;
(4)(x﹣5)3+8=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】教材中有如下一段文字: 思考
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC,固定住长木棍,转动短木棍,得到△ABD,这个实验说明了什么?
如图中的△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等.这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等.
小明通过对上述问题的再思考,提出:两边分别相等且这两边中较大边所对的角相等的两个三角形全等.请你判断小明的说法 . (填“正确”或“不正确”)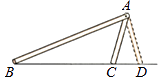
-
科目: 来源: 题型:
查看答案和解析>>【题目】平移前后的两个图形相互比较而言,下列说法正确的是( )
A. 两个图形大小不一样
B. 两个图形的形状不一样
C. 平移前比平移后小
D. 两个图形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】有若干张面积分别为a2、b2、ab的正方形和长方形纸片,小明从中抽取了1张面积为b2的正方形纸片,6张面积为ab的长方形纸片.若他想拼成一个大正方形,则还需要抽取面积为a2的正方形纸片( )
A.4张
B.8张
C.9张
D.10张 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x,y互为相反数,且|y﹣3|=0,求2(x3﹣2y2)﹣(x﹣3y)﹣(x﹣3y2+2x3)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系?小明通过观察分析,形成了如下解题思路:
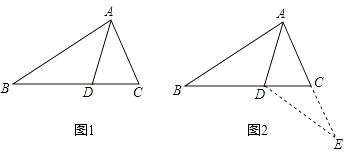
如图2,延长AC到E,使CE=CD,连接DE.由AB=AC+CD,可得AE=AB.又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB与∠ABC的数量关系.
(1)判定△ABD与△AED全等的依据是;
(2)∠ACB与∠ABC的数量关系为: .
相关试题

